Kalkulus Appletek

Primitív függvény a meredekségből és a határozatlan integrál

Megbizonyosodtunk az előzőekben arról, hogy a derivált határozott integrálja visszaadja az eredeti függvényt. Más szavakkal, ha f ' az f függvény deriváltja, akkor mondhatjuk, hogy f egy "antiderivált"-ja (azaz ptimitív függvénye) az f '-nek. Például, ha f (x) = x² akkor f '(x) = 2x. Így a 2x-nek egy "antiderivált"-ja az x². De, mivel a konstans deriváltja zérus, x² + 1 ugyanúgy egy "antideriváltja" (azaz egy primitív függvénye) a 2x-nek, ezek tükrében pontosan így mondhatjuk x² + C az "aniderivált", ahol C egy tetszőleges konstans. Tehát az általános "antideriváltja" egy fügvénynek valójában egy függvénycsalád, amelynek tagjai csak egy konstansban különböznek. A szokásos elnevezés szerint a primitív függvények halmazát határozatlan integrálnak vagy antideriváltnak nevezzük. Ez az applet megmutatja, hogyan kell megtalálni grafikusan az "atideriváltat". Gondoljunk úgy az integrandusra, mint egy primitív függvény meredekségére. A jelölése egy g függvény "antideriváltjának": 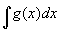, ezt a kifejezést nevezzük határozatlan integrálnak, mert nincsenek határai. Visszatérve a fenti példához, azt most így írnánk .

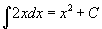Próbálja ki a következőket!

1. Ennek az appletnek a bal oldali grafikonján az integrandus f ' (x) = 2, egy konstans függvény. A jobb odali grafikon az "antideriváltat" mutatja, 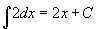. Tekintsen a bal oldali grafikonra úgy, hogy az ábrázolja a jobb oldali grafikon meredekségét. Vegye észre, hogy a bal oldali grafikon konstans, azaz a jobb oldali függvény meredeksége konstans, ez tehát egy egyenes lesz, melynek meredeksége 2! Mozgassa a C csúszkát! Mi történik a grafikonnal? Ha fordított irányban gondolkodunk, azaz a bal oldali grafikon a jobb odalon lévő függvény deriváltját mutatja, akkor érthető, hogy C nincs befolyással a bal oldali grafikonra.
   
   
2. Nézzük a 2. példát a legördülő listáról! Az integrandus változtatja az értékét -1-ről 1-re az x = 0-ban. Az "antiderivált" a jobb oldalon ennek következtében megváltoztatja a meredekségét -1-ről 1-re az x = 0-ban. Mozgassa az x cúszkáját! Ennek következtében a bal oldali grafikonon a keresztvonal mozogni fog (ennek most csak a függőleges része látszódik) míg a jobb oldali grafikonon a pont és a fekete iránytangens egyenese (azaz érintője) mozog. Látható az érintőből, hogy az "antiderivált" meredeksége változik.
   
   
3. Nézzük a 3. példát a legördülő listáról! Ebben a példában az integrandus függvény 1-től lefelé ereszkedő egyenes x = 1-ben. Mozdítsuk x csúszkáját és figyeljük mi történik az "antiderivált" érintőjével! Az érintő 1 meredekséggel indul, de ezután zérusra csökken. Mi történik ekkor a bal oldali grafikonon? Mi történik akkor, ha az x csúszkát túl toljuk ezen a ponton? Gondoljunk most úgy az integrandusra, mint az "antiderivált" meredeksége egy adott x értékű pontban. Az eredmény a primitív függvények halmaza, melyeket a grafikonon C különböző értékei adják meg (mozgassa C csúszkáját, változtassa a grafikonon a különböző primitív függvényeket).
   
   
4. Nézzük a 4. példát, amely két egyenesből felépülő integrandust mutat! Mozgassa az x csúszkát és figyelje meg, hogy az integrandus értéke (bal oldalon) hogyan mutatja az "antiderivált" meredekségét (jobb oldalon).

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.