Kalkulus Appletek

A határozott integrál tulajdonságai

Láthattuk, hogy a határozott integrál a Riemann összeg határértéke, úgy értelmezhető, mint a görbe alatti terület (a görbe és a vízszintes tengely közötti) előjeles területek összege. Ebben az appletben bemutatjuk néhány tulajdonságát a határozott integrálnak, ami hasznos lesz az integrál értékének kiszámításakor.

Próbálja ki a következőket!

1. Az applet egy exponenciális függvényt ábrázol, a görbe alatti terület a-tól b-ig zöld színnel van jelölve. Az a vagy b csúszkáját elmozdítva állítsuk be az a = b esetet. Mi ilyenkor a terület? Ez illusztrálja a zérus szabályt, .
   
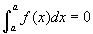   Most a csúszka segítségével állítsunk elő egy b < a relációnak megfelelő esetet! Mi történik a területtel? Ahogy látható, a határozott integrál határainak megcserélésével a terület előjelet vált, azaz .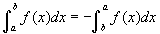
   
   
2. Válasszuk ki a 2. példát a legördülő listáról! Ez egy zöld egyenest és az a és b közötti intervallumhoz tartozó területet ugyancsak zöld színnel mutatja. Továbbá látható egy másik egyenes, pirossal, amely c-szerese az előző (zöld) függvénynek (h(x) = cf (x)). Kezdetben c = 2. Mit vehetünk észre a területeket tekintve (a terület értékek a grafikon bal felső sarkában találhatóak)? Mozgassuk c csúszkáját, vagy írjunk be különböző értékeket a c mezőbe. Mit veszünk észre? Próbáljuk ki azt az esetet, amikor c éppen -1. Ez jól mutatja a konstanssal való szorzás szabályát 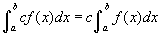. Másként fogalmazva, ha a határozott integrál integrandusa egy konstanssal van megszorozva, akkor "kivihetjük a konstanst" az integráljel elé.
   
   
3. Válasszuk ki a 3. példát. A zöld függvény egyenes f (x) = x, a kék görbe egy exponencális fügény g(x) = e^x és a piros görbe az összegük h(x) = f (x) + g(x). Mit veszünk észre a területtel kapcsolatban? Mozgassa az a és a b csúszkát és figyelje meg, hogy a kapcsolat még mindig igaz-e. Észre kellene vennie, hogy a piros görbe alatti terület egyenlő a kék és a zöld göbe alatti területek összegével. Ez természetesen érthető, hiszen a Riemann összegek éppen a vékony és magas téglalapok összegéből állnak, és a piros téglalapok magassága éppen a kék és a zöld téglalapok magasságának összege. Jelekkel: 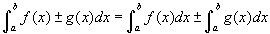. Ez azt állítja, hogy a két függvény összegének integrálja egyenlő a függvények integráljainak összegével. Az egyenlőségben plussz/mínusz szerepel, mivel a szabály érvényes két függvény különbségére is (szerkessze át a definíciós ablakban h(x)-t, legyen f (x) - g(x)).
   
   
4. Válasszuk ki a 4. példát! A grafikon az f (x) = e^x függvényt mutatja. A zöld terület a-tól c-ig és a kék terület c-től b-ig adja meg a görbe alatti területet. A két terület értékét, és az a-tól b-ig terjedő terület értékét a grafikon bal felső sarkában találja. Mit vesz észre, mi a kapcsolat a területek között? Változtassa a c csúszkát és figyelje, hogy a kapcsolat fennáll-e, ha c az a és b között helyezkedik el! Most húzza c-t a-n vagy b-n túl; még mindig fennáll a kapcsolat? Ezt belső összegzésnek nevezzük vagy 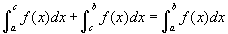. Szavakkal, a határozott integrált fel lehet osztani két intgrál összegére, melyeknek azonos az integrandusa, de a határok különbözőek, amint a példában láttuk a szabály igaz.
   
   
5. Válasszuk ki az 5. példát! A zöld görbe egy exponenciális függvény f (x) = ½ e^x és a kék görbe ugyancsak egy exponenciális függvény g(x) = e^x. Az a-tól b-ig terjedő intervallumon g(x) mindig nagyobb, mint f (x). Ez azt jelenti, hogy a Riemann összeg téglalapjai g(x)-re mindig magasabbak, mint az f (x) esetén. Ezért a g alatti terület nagyobb lesz, mint az f alatti terület, amint látja ez ebben az esetben igaz. Ha g(x) ≥ f (x) az [a,b] zárt intervallumon, akkor 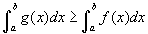. Vegyük az f (x) = 0 speciális esetet! Írja be f definíciós ablakába, majd üssön Enter-t! Az állítás tehát az, hogy ha g pozitív minden intervallumon, akkor a határozott integrál is pozitív lesz ugyanazon az intervallumon.
   
   
6. Válasszuk ki a 6. példát! Az f (x) = e^x függvény zöld. A zöldes szürke téglalap magassága az f minimum értéke [a,b] zárt intervalumon, míg a sötét szürke téglalap magassága az f maximum értéke ugyanazon az intervallumon. Világos, hogy az f alatti terület valahol a két téglalap területe között van. Matematikailag azt mondjuk 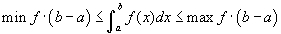, ahol min f az f függnény minimum értéke az [a,b] intervallumon és max f az f maximum értéke ezen az intervallumon. Az intervallum és a téglalapok szélessége (b - a).
   
   
7. Válasszuk ki a 7. példát! Itt két egyenes közötti területet láthatunk, ahol az f (x) a felső függvény (zöld) és az alatta lévő g(x) függvény (kék). Kétféleképpen gondolkodhatunk a két egyenes közötti területről. Megadjuk a felső függvény alatti területet, majd ebből kionjuk az alsó függvény alatti területet, vagy 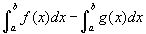. Ugyancsak elgondolkodhat azon a lehetőségen, hogy megadjon egy olyan Riemann összeget, ahol a téglalap teteje a felső függvényen van, az alja az alsó függvényen. Ekkor a téglalapok magassága f (x) - g(x), így a terület .
   
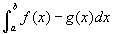   Változtassa meg a g(x) fügvényt úgy, hogy tegyen egy mínusz jelet az elejére (azaz legyen - 0.5x) és üssön Enter-t! Van értelme annak, hogy a két görbe közötti terület nagyobb lett? Törölje a mínusz jelet maradjon az eredeti (azaz g(x) = 0.5x) és legyen f (x) = - x (azaz tegyen egy mínusz jelet f elé és üssön Enter-t)! Mi történik a területtel? Miért lesz a terület negatív, amikor "felső" függvény valójában alatta van a "alsó" függvénynek?
   
   
8. Válasszuk ki a 8. példát! Ez egy bonyolultabb esetet mutat, a két függvény metszi egymást. A bal oldali terület a metszésponttól negatív lesz, mivel g(x) nagyobb ezen a részintervallumon, ugyanakkor a metszésponttól jobbra eső terület pozitív lesz, mivel f (x) a nagyobb.
   
   
9. Kísérletezhet a saját függvényeivel, a választási ablakban kiválaszthatja a tulajdonságokat; kialakíthatja a bemeneti ablakban, vagy csúszkákkal a grafikonnak megfelelően. Bevezetheti a függvény definícióját, az a értékét, b értékét, és c értékét (ami megfelelő a példának) valamint tudja kicsinyíteni, nagyítani és mozgatni az ábrát.

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.