Ívhossz
Láttuk, hogy a Riemann összeg használható a terület és a térfogat közelítésére. A határozott integrál a Riemann összeg határértéke az intervallum felosztásának finomítása és növelése mellett, így megkapjuk a keresett területet vagy térfogatot. Hasonló technikát alkalmazhatunk függvénygörbe hosszának meghatározásához. Természetesen ha a fügvény grafikonja egyenes, akkor az egyenes egy darabjának a hosszát az ismert távolság összefüggés alapján határozzuk meg. Amennyiben egy görbe hosszát szeretnénk magadni közelítőleg, felosztjuk a görbét és kis szakaszokkal közeltjük a görbe darabokat. Amint a felosztásunk egyre finomabb lesz, azaz a darabok zérushoz tartank használhatjuk a határozott integrált, hogy megtaláljuk a görbe ívosszát.
Próbálja ki a következőket!
- A bevezető példa a parabola egy ívét ábrázolja. Először közelítsük a hosszát egy egyenes szakasszal, mely a végpontokhoz igazodik. Láthatóan ez nem túl jó közelítés, de javíthatunk rajta, ha növeljük a szakaszok számát. Mozgassa az intervallum csúszkát, amellyel növelni tudja a húrok számát, és láthatja, hogy a feketével húzott húrok hosszainak az összege egyre közelebbi érték lesz a magenta színű görbe hosszához! Vegye észre, hogy a közelítő hosszúság egyre közelebb kerül a tényleges hosszúsághoz! Amennyiben Δx jelöi a végpontok közötti szakaszos felosztás x szerinti változását és Δy a változást y szerint, akkor egy darab szakasz hossza a távolságra vonatkozó összefüggés alapján
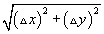 . Sajnos ez nem egy Riemann összeg eleme, amely egy változó függvénye szorozva a változó pici intervallumával. Azonban algebrai úton át tujuk alakítani az összefüggést, úgy hogy Δx-et kiemelünk a gyökjel alól
. Sajnos ez nem egy Riemann összeg eleme, amely egy változó függvénye szorozva a változó pici intervallumával. Azonban algebrai úton át tujuk alakítani az összefüggést, úgy hogy Δx-et kiemelünk a gyökjel alól 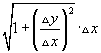 . Összegezve ezeket és véve a határértéket, amint Δx tart zérushoz a határozott integrál
. Összegezve ezeket és véve a határértéket, amint Δx tart zérushoz a határozott integrál 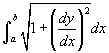 , ahol a < b. Mivel dy/dx = f '(x) ha f az a függvény, amelyiknek az ívhosszát mérjük, akkor kézenfekvő az integrált így írni:
, ahol a < b. Mivel dy/dx = f '(x) ha f az a függvény, amelyiknek az ívhosszát mérjük, akkor kézenfekvő az integrált így írni: 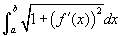 . A példában ez az integrál:
. A példában ez az integrál: 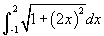 , ahol 2x az x² deriváltja. Könnyen látható, hogy az ivhosszhoz tartozó integrálhoz nem könnyű megtalálni a primitív függvényt, így általában a legegyszerűbb numerikusan meghatározni az integrált.
, ahol 2x az x² deriváltja. Könnyen látható, hogy az ivhosszhoz tartozó integrálhoz nem könnyű megtalálni a primitív függvényt, így általában a legegyszerűbb numerikusan meghatározni az integrált.
- Nézzük a 2. példát a legördülő listáról! Ez alapvetően ugyanaz a példa, mint az előző, kivéve hogy most x az y függvéye. Az általános formula
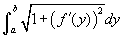 és a konkrét példára
és a konkrét példára 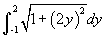 . A hosszúság ugyanaz lesz, mivel ez a példa ugyanaz, mint az első példa csak az y = x egyenesre van tükrözve.
. A hosszúság ugyanaz lesz, mivel ez a példa ugyanaz, mint az első példa csak az y = x egyenesre van tükrözve.
- Nézzük a 3. példát a legördülő listáról, ami egy paraméterses görbét mutat! Ez a görbe egy félkör (ha kicsit deformátnak látja, klikkeljen az Equalize Axes gombra). Mozgassa az "intervals" csúszát, hogy a közelítés jobban meközelítse a tényleges ívhosszt, amelynek értéke a geometriából ismert: π! Mivel a független változó a paraméteres egyenletekben t, visszatérhetünk az eredeti távolság összefüggéshez
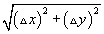 kiemelve Δt -t a gyökjel alól:
kiemelve Δt -t a gyökjel alól: 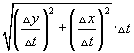 . Összegezve, majd véve a határértéket, amint Δt tart zérushoz az integrál
. Összegezve, majd véve a határértéket, amint Δt tart zérushoz az integrál 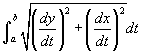 . Vegye észre, hogy a és b a t határai nem x-beli határok! A megoldás meghatározásához behelyettesítjük a deriváltakat
. Vegye észre, hogy a és b a t határai nem x-beli határok! A megoldás meghatározásához behelyettesítjük a deriváltakat 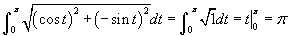 . Látható hogy ez az integrál pontosan kiszámolható, ha alkalmazzuk a Pitagorasz tételt az egyszerűsítésre.
. Látható hogy ez az integrál pontosan kiszámolható, ha alkalmazzuk a Pitagorasz tételt az egyszerűsítésre.
- Nézzük a 4. példát a legördülő listáról! Ebben a példában th-t használunk θ helyett, hogy egyszerűbb legyen a leírása. Mozgassa az "intervals" csúszát, hogy a közelítés jobban meközelítse a tényleges ívhosszt, amint növeli a beosztások számát! Az ívhossz meghatározásához először alakítsuk át a poláris egyenletet r = f (θ) két paraméteres egyenletté x = f (θ)cosθ és y = f (θ)sinθ. Ezután használjuk a parametrikus ívhossz formulát
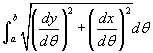 , amelyben a két parametrikus egyenlet deriváltját találja. Jelen példánkban
, amelyben a két parametrikus egyenlet deriváltját találja. Jelen példánkban 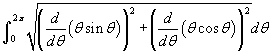 , amelyet a legegyszerűbb numerikusan kiszámolni (lehetséges az integrandus egyszerűsítése a deriváltak beírása után, használva a Pitagorasz tételt, de az így kapott integrandust se könnyű integrálni).
, amelyet a legegyszerűbb numerikusan kiszámolni (lehetséges az integrandus egyszerűsítése a deriváltak beírása után, használva a Pitagorasz tételt, de az így kapott integrandust se könnyű integrálni).
- Ebben a részben ki tudja próbálni saját függvényét, ki tudja választani a görbe típusát (normál, inverz, paraméteres, polár), majd ki tudja választani a és b értékét, tud kicsinyíteni, nagyítani, mozgatni az ablakot a szokásos módon. Megjegyezzük, hogy amennyiben a > b a választása, akkor az eredmény negatív lesz. Mivel a hoszúságot pozitívnak definiáljuk, ezért figyeljen arra, hogy a < b legyen.

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.
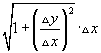 . Összegezve ezeket és véve a határértéket, amint Δx tart zérushoz a határozott integrál
. Összegezve ezeket és véve a határértéket, amint Δx tart zérushoz a határozott integrál 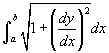 , ahol a < b. Mivel dy/dx = f '(x) ha f az a függvény, amelyiknek az ívhosszát mérjük, akkor kézenfekvő az integrált így írni:
, ahol a < b. Mivel dy/dx = f '(x) ha f az a függvény, amelyiknek az ívhosszát mérjük, akkor kézenfekvő az integrált így írni: 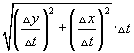 . Összegezve, majd véve a határértéket, amint Δt tart zérushoz az integrál
. Összegezve, majd véve a határértéket, amint Δt tart zérushoz az integrál 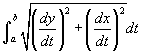 . Vegye észre, hogy a és b a t határai nem x-beli határok! A megoldás meghatározásához behelyettesítjük a deriváltakat
. Vegye észre, hogy a és b a t határai nem x-beli határok! A megoldás meghatározásához behelyettesítjük a deriváltakat 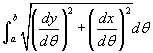 , amelyben a két parametrikus egyenlet deriváltját találja. Jelen példánkban
, amelyben a két parametrikus egyenlet deriváltját találja. Jelen példánkban 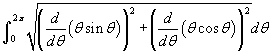 , amelyet a legegyszerűbb numerikusan kiszámolni (lehetséges az integrandus egyszerűsítése a deriváltak beírása után, használva a Pitagorasz tételt, de az így kapott integrandust se könnyű integrálni).
, amelyet a legegyszerűbb numerikusan kiszámolni (lehetséges az integrandus egyszerűsítése a deriváltak beírása után, használva a Pitagorasz tételt, de az így kapott integrandust se könnyű integrálni). 