Polárkoordinátás görbe területe
Az integrálást polárkoordinátákkal megadott görbe által közrefogott terület megadására ugyancsak tudjuk használni. Ebben az esetben azonban körcikkeket használunk téglalapok helyett a terület megadásához.
Próbálja ki a következőket!
- Az applet elsőként egy kört ábrázol, mely az r = 1 polár egyenletével van megadva. Geometriából tudjuk, hogy a területe egy ilyen körnek π. Meg lehet közelíteni ezt a területet, ha kis szögtartomány részekre bontjuk, melyet a szürke terület ábrázol. Mozgassa a th csúszkát (th-t használunk θ helyett, hogy könnyebb legyen a polárkoordinátás egyenletek gépelése) és figyelje hogyan mozog a körcikk! A dθ szögű és r sugarú körcikk területe ½ r² dθ. Amennyiben összeadjuk a körcikkek területét és dθ tart zérushoz, az integrál
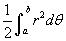, ahol r helyére beírjuk a konkrét görbe polárkoordinátás egyenletét θ függvényében. Ebben a példában az integrál: 
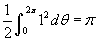. Megjegyezük, hogy a polárkoordinátás területszámításnál a-nak nagyobbnak kell lennie, mint b, hasonlóan az ívhosz megadásánál (egyébként az integrállal kapott terület negatív lesz). Van egy másik dolog is amire figyelni kell, az integrál nem fog helyes eredményt adni, ha a görbe fedésbe kerül önmagával, vagy ha a zárt terület többszörösen fedésben van. Például, ha b értékének 4pi-t adunk, b ablakába ezt gépeljük be, a terület kétszeresét adja meg annak, aminek lennie kellene. Ez azért van mert θ 0 és 2π közötti értékeket vehet fel, így lesz meg a teljes szög; ha θ 0 -tól 4π-ig mehet, akkor kétszer teszi meg a teljes kört, és kétszer fedi le a kört.
- Nézzük a 2. példát a legördülő listáról, amely egy csigavonalat ábrázol! Egyenlete r = θ . Mozgassa a th csúszkát, és figyelje meg a szögtartomány mozgását, vegye észre, hogy a sugár nem állandó, θ-val együtt változik! Az integrál ebben az esetben
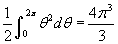. Mozgassa a b csúszkát, amely a felső határt változtatja és figyelje hogyan válozik a sárgával színezett terület! Ez a reguláris görbék alatti területhez képest eltérő, mivel ott a sárga terület határoló vonala az y tengellyel párhuzamos, itt viszont a határoló vonalak az origón haladnak keresztül.
- Nézzük a 3. példát, amely a "rózsa", vagy ismertebb nevén a lóhere görbét ábrázolja. Mozgassa th csúszkáját, hogy lássa az egyes szektorok hogyan adódnak össze. Az integrál ebben az esetben
.
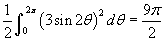- Ki tudja próbálni saját görbéit, ha beírja az egyenleteket (használja a th-t θ jelölésére), adja meg a és b olyan értékeit, amit szeretne, és kicsinyítsen, nagyítson, valamint mozgassa az ablakot igénye szerint! Megjegyezzük, hogy gondolja meg mit választ a és b értéknek, hogy a tényleges területet, amit szeretne tudni, megkapja és elkerülje a kétszeres számolást (használja a csúszkát segítségként, hogy lássa hol a határ; ha a vagy b értékét a 0 és 2π tartományon túl szeretné használni, akkor a és b ablakait használja a csúszka helyett).
This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.