Ismert keresztmetszetű térfogatok
A előző részben megmutattuk, hogyan kell meghatározni egy olyan testnek a térfogatát, amit úgy kapunk, hogy két görbe által közbezárt területet megforgattunk egy tengely körül. Ebben a részben olyan testek téfogatát vizsgáljuk meg, amelyeknek a keresztmetszete ismert, de ne nem forgatással kaptuk.
Próbálja ki a következőket!
- Az applet először egy sárgával jelölt, az f (x) = x +1 és a g(x) = x² függvények által határolt területet mutat 0-tól 1-ig. Ez az alapja azoknak a testeknek, amelyeknek négyzet a keresztmetszete és ez merőleges az x tengelyre (vagyis az egyik oldala a négyzetnek a sárga treületen halad át). Mozgassa az x csúszkát, amely egy szeletet mozgat a megadott tartományon, vegye észre, hogy a négyzet oldala változik! A két végponton egy-egy világosszürke négyzetet lát. Megjegyezzük, hogy a képablakban a négyzet téglalapnak látszódik a perspektíva miatt. A térfogata egy vékony négyzet szeletnek, melynek a vastagsága dx a négyzet oldala pedig s, egynlő a terület szorozva a dx vastagsággal, azaz s²dx. De s éppen a távolság a két görbe között egy adott x helyen, vagyis s = x +1 - x². Így, az integrál, amely öszegzi ezeket a térfogatokat:
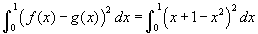 . Az olvasónak adjuk azt a házi feladatot, hogy belássa a végeredmény 41/30, amely közelítőleg 1.367.
. Az olvasónak adjuk azt a házi feladatot, hogy belássa a végeredmény 41/30, amely közelítőleg 1.367.
- Nézzük a 2. példát a legördülő listáról, amely ugyanazt a területet ábrázolja! Most azonban a keresztmetszet (amely merőleges az x tengelyre) olyan négyzet, amelynek az átlója fekszik a sárga területen. Ez azt jelenti, hogy a négyzet szelet a képablak síkjából kinyúlik és mögé is nyúlik. Mozgassa az x csúszkát, amely a kersztmetszet szeletet fogja mozgatni az adott tartományon, figyelje meg, hogyan változik a mérete! Egy ilyen szelet térfogata, a dx vastagsággal és a d átló hosszúsággal, éppen a dx vastagság szorzva a területtel, azaz d²/2dx. De d a két görbe közötti távolság egy adott x helyen, így d = x +1 - x². Az integrál, amely ezeket a szeleteket összegzi
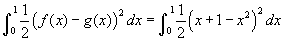 . Legyen házi feladat belátni, hogy az eredmény 41/60, amely közelítőleg 0.683.
. Legyen házi feladat belátni, hogy az eredmény 41/60, amely közelítőleg 0.683.
- Nézzük a 3. példát a legördülő listáról! Most a keresztmetszet (amely merőleges az x tengelyre) félkör, amelynek az átmérője fekszik a sárga területen. Ez azt jelenti, hogy a vékony szelet kinyúlik a képablak síkjából. Mozgassa az x csúszkát, amellyel a szürke szeletet mozgatja a megadott tartományon. Egy szelet térfogata, dx vastagsággal és d hosszúságú átmérővel, a terület szorozva a dx vastagsággal, azaz π(d/2)²/2dx. De d éppen a két görbe közötti távolság egy adott x helyen, azaz d = x +1 - x². Az integrál, amely ezeket a szeleteket összegzi:
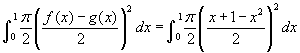 . Legyen házi feladat belátni, hogy az eredmény 41π/240, amely közelítőleg 0.537.
. Legyen házi feladat belátni, hogy az eredmény 41π/240, amely közelítőleg 0.537.
- Nézzük a 4. példát a legördülő listáról! Ebben a példában a keresztmetszet (amely merőleges az x tengelyre) kör, amelynek az átmérője a sárga területen van. Ez azt jelenti, hogy a kör szelet a képablak síkjából kinyúlik és mögé is nyúlik. Mozgassa az x csúszkát amely a szürke szeletet fogja mozgatni az adott tartományon, figyelje meg hogyan változik a mérete! Egy ilyen szelet térfogata, a dx vastagsággal és a d hosszúságú átmérővel, a kör területe szorozva a dx vastagsággal, azaz π(d/2)²dx. De d éppen a két görbe közötti távolság egy adott x helyen, azaz d = x +1 - x². Az integrál, amely ezeket a szeleteket összegzi:
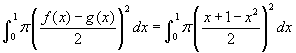 . Legyen házi feladat belátni, hogy az eredmény 41π/120, amely közelítőleg 1.073. Megjegyezzük, hogy ez a példa különbözik áttól, amikor egy tengely körüli forgatással kaptunk testet; ebben a példában nincsen olyan egyenes, amely tengely lehetne.
. Legyen házi feladat belátni, hogy az eredmény 41π/120, amely közelítőleg 1.073. Megjegyezzük, hogy ez a példa különbözik áttól, amikor egy tengely körüli forgatással kaptunk testet; ebben a példában nincsen olyan egyenes, amely tengely lehetne.
- Nézzük a 5. példát a legördülő listáról! A keresztmetszet (amely merőleges az x tengelyre) egyenlő oldalú háromszög, amelynek az egyk oldala a sárga területen van. Ez azt jelenti, hogy a háromszög szelet a képablak síkjából kinyúlik. Mozgassa az x csúszkát amely a szürke szeletet fogja mozgatni az adott tartományon, figyelje meg hogyan változik a mérete! Egy ilyen szelet térfogata, a dx vastagsággal és az s oldalhosszal, a háromszög területete szorozva a dx vastagsággal, azaz
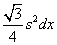 . De s éppen a két görbe közötti távolság egy adott x helyen, azaz s =x +1 - x². Az integrál, amely ezeket a szeleteket összegzi:
. De s éppen a két görbe közötti távolság egy adott x helyen, azaz s =x +1 - x². Az integrál, amely ezeket a szeleteket összegzi: 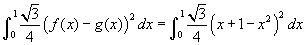 . Legyen házi feladat belátni, hogy az eredmény 41√3/120, amely közelítőleg 0.592.
. Legyen házi feladat belátni, hogy az eredmény 41√3/120, amely közelítőleg 0.592.
- Nézzük a 6. példát a legördülő listáról! A keresztmetszet (amely merőleges az x tengelyre) egyenlő szárú derékszögű háromszög, amelynek az átfogója fekszik a sárga területen. Ez azt jelenti, hogy a derékszögű csúcs a képablak síkjából kinyúlik. Mozgassa az x csúszkát amely a szürke szeletet fogja mozgatni az adott tartományon, figyelje meg hogyan változik a mérete! Egy ilyen szelet térfogata, a dx vastagsággal és a h alap hosszával, a háromszög területete szorozva a dx vastagsággal, azaz h²/4dx. De h éppen a két görbe közötti távolság egy adott x helyen, azaz h = x +1 - x². Az integrál, amely ezeket a szeleteket összegzi:
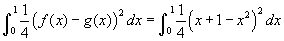 . Legyen házi feladat belátni, hogy az eredmény 41/120, amely közelítőleg 0.342.
. Legyen házi feladat belátni, hogy az eredmény 41/120, amely közelítőleg 0.342.
- Nézzük a 7. példát a legördülő listáról! A keresztmetszet (amely merőleges az x tengelyre) egyenlő szárú derékszögű háromszög, amelynek az egyik szára fekszik a sárga területen. Ez azt jelenti, hogy a másik szár és az átfogó a képablak síkjából kinyúlik. Mozgassa az x csúszkát amely a szürke szeletet fogja mozgatni az adott tartományon, figyelje meg hogyan változik a mérete! Egy ilyen szelet térfogata, a dx vastagsággal és l oldalhosszal a háromszög területete szorozva a dx, vagy l²/2dx. De l éppen a két görbe közötti távolság egy adott x helyen, azaz l = x +1 - x². Az integrál, amely ezeket a szeleteket összegzi:
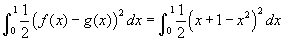 . Legyen házi feladat belátni, hogy az eredmény 41/60, amely közelítőleg 0.683.
. Legyen házi feladat belátni, hogy az eredmény 41/60, amely közelítőleg 0.683.
- Nézzük a 8. példát! Ebben a példában a függvény y-tól függ x helyett és a keresztmetszet az y tengelyre merőleges. Bevezetőül négyzet kersztmetszetet választottunk. Mozgassa az y csúszkát amely a szürke szeletet fogja mozgatni az adott tartományon, figyelje meg hogyan változik a mérete! Az integrál, amely ezeket a szeleteket összegzi:
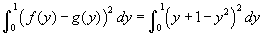 . Ahogy az várható volt (mivel a tartomány ugyanaz, mint az 1. példában, csak x és y van felcserélve), a terület az 1. példában lévő területtel megegyező. Használhatja a legördülő listát, ahol más keresztmetszeteket is kipróbálhat!
. Ahogy az várható volt (mivel a tartomány ugyanaz, mint az 1. példában, csak x és y van felcserélve), a terület az 1. példában lévő területtel megegyező. Használhatja a legördülő listát, ahol más keresztmetszeteket is kipróbálhat!
- Nézzük a 9. példát! Ebben a részben kipróbálhatja saját függvényeit, választhat integrációs határokat, keresztmetszet alakot, és eldöntheti, hogy x-et vagy y-t választja változónak (ne feledje, amennyiben y-t választja változónak klikkeljen az "inverse" ablakra).

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.
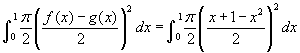 . Legyen házi feladat belátni, hogy az eredmény 41π/240, amely közelítőleg 0.537.
. Legyen házi feladat belátni, hogy az eredmény 41π/240, amely közelítőleg 0.537.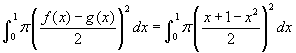 . Legyen házi feladat belátni, hogy az eredmény 41π/120, amely közelítőleg 1.073. Megjegyezzük, hogy ez a példa különbözik áttól, amikor egy tengely körüli forgatással kaptunk testet; ebben a példában nincsen olyan egyenes, amely tengely lehetne.
. Legyen házi feladat belátni, hogy az eredmény 41π/120, amely közelítőleg 1.073. Megjegyezzük, hogy ez a példa különbözik áttól, amikor egy tengely körüli forgatással kaptunk testet; ebben a példában nincsen olyan egyenes, amely tengely lehetne.