Átlagsebesség és gyorsaság
Vessünk egy pillantást az átlagsebességre! Ha visszaemlékezünk korábbi matematikai tanulmányainkra,
az átlagos sebesség nem más, mint a megtett távolság osztva az idővel. Például ha egy tárgyat feldobunk a levegőbe,
az alábbi adatokat kapjuk a tárgy lábakban (röv.: ft) kifejezett y magasságra a másodpercekben (röv.: sec) kifejezett t idő függvényeként,
ha a kilövés pillanatában t = 0 volt:
| t (sec) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| y (ft) |
6 |
90 |
142 |
162 |
150 |
106 |
30 |
A táblázat azt mutatja, hogy a tárgy 6 láb magasan volt a föld felett, amikor felhajítottuk,
1 másodperccel később 90 láb magasan volt, stb. Milyen gyorsan repült? A megtett távolságot az idővel elosztva kapjuk meg a sebességet.
Például az első másodpercben az átlagsebesség: 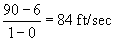 . Az utolsó másodpercben az átlagsebesség:
. Az utolsó másodpercben az átlagsebesség: 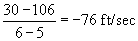 . Megjegyezzük, hogy a sebesség lehet negatív is, ami a lefele mozgást jelöli
(esetünkben a pozitív sebesség emelkedő mozgást jelez). A gyorsaság nem más, mint a sebesség nagysága (vagyis
a jelen egydimenziós esetben az abszolútértéke). Ki tudjuk számolni a teljes intervallumra eső átlagsebességet is, íme:
. Megjegyezzük, hogy a sebesség lehet negatív is, ami a lefele mozgást jelöli
(esetünkben a pozitív sebesség emelkedő mozgást jelez). A gyorsaság nem más, mint a sebesség nagysága (vagyis
a jelen egydimenziós esetben az abszolútértéke). Ki tudjuk számolni a teljes intervallumra eső átlagsebességet is, íme:
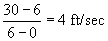 .
.
Mármost mi van akkor, ha egy konkrét időpontbeli, mondjuk a t = 1 időpontbeli sebességet szeretnénk megtudni?
Nyilvánvalóan valamilyen sebesség ez, hiszen a tárgy mozog, ám a sebesség kiszámításához a megtett távolság és az eközben eltelt idő arányára van szükségünk. Meg tudnánk határozni az 1. és 2. másodperc közötti időintervallumra eső átlagsebességet, ami 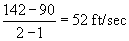 . Ám ez nemigen lehet a helyes válasz, miután a tárgy láthatólag gyorsul.
Ha rendelkeznénk olyan magasság adattal, ami közelebb esik az 1. másodperchez, jobb becslést adhatnánk a t = 1 időpontbeli pillanatnyi sebességre.
Az alábbi applet ezt mutatja be.
. Ám ez nemigen lehet a helyes válasz, miután a tárgy láthatólag gyorsul.
Ha rendelkeznénk olyan magasság adattal, ami közelebb esik az 1. másodperchez, jobb becslést adhatnánk a t = 1 időpontbeli pillanatnyi sebességre.
Az alábbi applet ezt mutatja be.
Próbálja ki a következőket:
- Az applet a fenti táblázat egy részhalmazát mutatja. Az alján talál egy h értéket egy hozzá tartozó
mezővel és egy állítható csúszkával. A táblázat első sora az időt mutatja az 1. másodpercben
és az 1 + h-adik másodpercekben. A második sor a magaságot mutatja e két időpontban, a harmadik pedig
kiszámolja az erre az intervallumra eső átlagsebességet. Az applet kiinduló állapotában a h = 1 értékkel éppen
az 1. és 2. másodperc közötti átlagsebességet mutatja, amit fentebb már meghatároztunk.
- Állítsa a h csúszkát kisebb értékekre! Ezzel egy kisebb intervallumhoz jut, így az átlagsebesség
jobban meg fogja közelíteni a t = 1 időpontbeli pillanatnyi sebességet. Állítsa a h-t
egyre kisebbre! Mi történik a sebességgel? Közelít-e valamilyen számhoz?
- A csúszkát teljesen balra tolva tegye a h értékét 0-vá! Mi történik a sebességgel? Miért?
- Írja be a 0.001 értéket a h mezőbe, és nyomjon Enter-t! Aztán próbálja ki ugyanezt 0.0001 értékkel, stb.
Milyen számhoz közelít a sebesség, ahogyan h közelít 0-hoz?
- Megjegyzendő, hogy ha a h kisebb vagy egyenlővé válik mint 0.000000001, a kerekítési hibák már problémákat okoznak.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
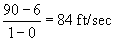 . Az utolsó másodpercben az átlagsebesség:
. Az utolsó másodpercben az átlagsebesség: 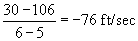 . Megjegyezzük, hogy a sebesség lehet negatív is, ami a lefele mozgást jelöli
(esetünkben a pozitív sebesség emelkedő mozgást jelez). A gyorsaság nem más, mint a sebesség nagysága (vagyis
a jelen egydimenziós esetben az abszolútértéke). Ki tudjuk számolni a teljes intervallumra eső átlagsebességet is, íme:
. Megjegyezzük, hogy a sebesség lehet negatív is, ami a lefele mozgást jelöli
(esetünkben a pozitív sebesség emelkedő mozgást jelez). A gyorsaság nem más, mint a sebesség nagysága (vagyis
a jelen egydimenziós esetben az abszolútértéke). Ki tudjuk számolni a teljes intervallumra eső átlagsebességet is, íme:
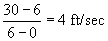 .
.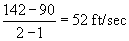 . Ám ez nemigen lehet a helyes válasz, miután a tárgy láthatólag gyorsul.
Ha rendelkeznénk olyan magasság adattal, ami közelebb esik az 1. másodperchez, jobb becslést adhatnánk a t = 1 időpontbeli pillanatnyi sebességre.
Az alábbi applet ezt mutatja be.
. Ám ez nemigen lehet a helyes válasz, miután a tárgy láthatólag gyorsul.
Ha rendelkeznénk olyan magasság adattal, ami közelebb esik az 1. másodperchez, jobb becslést adhatnánk a t = 1 időpontbeli pillanatnyi sebességre.
Az alábbi applet ezt mutatja be.