Kalkulus appletek

A folytonosság formális meghatározása

Most hogy szert tettünk a határérték formális definíciójára, felhasználhatjuk ezt a folytonosság formálisabb meghatározásához. Egy függvénynek valamely pontban való folytonosságát a következőképpen definiálhatjuk:

Az f függvény folytonos az x = c helyen, ha f (c) létezik és ha .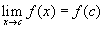

Más szóval, egy függvény folytonos egy pontban, ha ott a függvényérték megegyezik a határértékkel. Az egy pontbeli folytonosság definícióját felhasználhatjuk a szakaszon folytonosság meghatározására, ti. a szakasz minden pontjában való folytonosságként.

Próbálja ki a következőket:

1. Az első grafikonon egy közönséges parabola látható. Tolja el a csúszkát egy tetszőleges x értékre! Figyelje meg, hogy az y = mezőben megjelenő függvényérték megegyezik a pontbeli határértékkel! Így a függvény folytonos ebben az x értékben. Mivel ez bármely kiválasztott x értékre igaz, ezért a függvény mindenütt folytonos.
   
   
2. Válassza ki a második példát a legördülő menüből! A szinuszgörbe már jobban tekergődzik, de még mindig folytonos. Tolja el a csúszkát egy tetszőleges x értékre! Mint az előző példánál, itt is bármilyen kimenő értéket néz, az azonos a határértékkel, így ez a függvény is mindenütt folytonos.
   
   
3. Válassza ki a harmadik példát! Ennek a függvénynek függőleges aszimptotája van az x = 1 helyen. Folytonos-e az x = 1 helyen? Mivel a függvény még csak értelemzve sincs itt, ezért a válasz nemleges. A folytonosság formális definíciója megköveteli, hogy a függvény értelmezve legyen a szóban forgó x értéknél.
   
   
4. Válassza ki a negyedik példát! Ez a függvény 1-ről 2-re ugrik az x = 1 helyen. Figyelje meg, hogy f (1) = 2, de a határérték az x = 1 helyen nem létezik (mivel a baloldali és a jobboldali határérték különböző)! Ezért ez a függvény nem folytonos az x = 1 helyen.
   
   
5. Válassza ki az ötödik példát! Ennek a függvénynek hézagpontja van az x = 1 helyen. Most a határérték létezik az x = 1 helyen (értéke 1), ám a függvény nem vesz fel itt értéket, ezért nem folytonos az x = 1 helyen.
   
   
6. Válassza ki a hatodik példát! Ennek a függvénynek áthelyeztük egy pontját az x = 1 helyen. Most a határérték létezik az x = 1 helyen (értéke 1), a függvény értéket vesz fel itt (f (1) = 2), de a határérték és a függvényérték különböznek. Így ez a függvény sem folytonos az x = 1 helyen.
   

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.