Alapintegrálok
Azt láttuk, hogy az általános "antiderivált"-ja egy függvény deriváltjának éppen maga a függvény plussz egy konstans. Ebből következően ki tudjuk számolni azokat az integrálokat, ahol az integrandus egy olyan drivált, amit már ismerünk.
Próbálja ki a következőket!
- Ez az applet a bal oldalon egy olyan grafikont mutat, ahol az integrandus konstans, mégpedig 0. Mozgassa az x csúszkát, azt látja, hogy nincs összeadódó terület! A legördülő listában két lehetőség közül válszthat: "Slope"(meredekség) ebben az esetben a példát (és más példákat is) a meredekség szemszögéből vizsgáljuk. Ebből a nézőpontból az 1. példában a meredekség mindig zérus, így az "antiderivált"-nak vízszintes egyenesnek kell lennie. Mozgassa a C csúszkát és figyelje a függvénycsaládot. Használva a határozatlan integrál jelölését, azt mondhatjuk, hogy
.
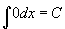- Nézzük a 2. példát! Itt az integrandus konstans, mégpedig 2! Mozgssa az x csúszkát, azt látja, hogy a terület lineárisan növekszik! "Slope" perspktívából nézve a meredekség konstans, azaz egy egyenes. Így
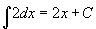. Általánosabban, ha k egy konstans, 
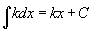. Ebben az appletben a pozitív területet zölddel, a negatív területet pirossal színeztük.
- Nézzük a 3. példát, ahol az integrandus egy egyenes! Mozgassa az x csúszkát és figyelje az akkumulálódó területet! Specálisan válassza az x = 1-et! Mi lesz ekkor az "antiderivált" értéke? Mivel ez az érték nem 1, az "antiderivált" nem lehet csak x², hanem
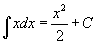-nek kell lennie. Ezt tudja ellenőrizni, ha az egyenlőségnek a jobb oldalát deriválja , látható, hogy eredményül éppen x-et kap.
- Nézzük a 4. példát, amely egy parabolát mutat! Vegyük újra az x = 1-et és figyeljük az "antiderivált" értékét. Mivel az értéke nem 1, az "antiderivált" nem lehet csak x³, hanem
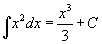-nek kell lennie. Ezt tudja ellenőrizni, ha az egyenlőségnek a jobb oldalát deriválja , látható, hogy eredményül éppen x²-et kapja.
- Nézzük az 5. példát, amely egy harmadfokú görbét mutat! Ki tudja találni az "antiderivált" függvényt? Talán meg tudja mondani az eddigi példák alapján mi az általános formula az "antiderivált"-ra hatványfüggvények esetében:
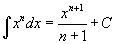. Próbálja meg deriválni az egyenlőség jobb oldalát, hogy belássa tényleg megkapja az integrandust!
- Nézzük a 6. példát, amely egy hiperbola 1/x (vagy x-1)! A hatványfüggvényre vonatkozó szabály most nem használható, mert akkor a nevező a jobb oldalon zérus lenne és a zérussal való osztás nem értelmezett. Mozgassa az x csúszkát, így látható, hogy a primitív függvény meredeksége megegyezik az integrandus értékével, hogy megnézze a merdekségét az "antiderivált"-nak és hasonlítsa össze az integrandus értékével (ez leginkább a "meredekség” nézetben látszik jól)! Melyik függvénynek a derváltja az 1/x? Talán emlékszik rá, hogy ez az ln(x) függvény. De, ez a példa egy kicsit más, mivel 1/x felvehet pozitív és negatív értékeket is. Ezért a szabály
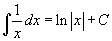, ahol az abszolút érték adja a megfelelő görbét a negatív oldalon. Amennyiben a terület perspektívájából vizsgáljuk a dolgokat és mozgatjuk az x csúszkát, észreveheti, hogy a terület 1 -gyel kezdődik 0 helyett. Mivel az integrandus nem értelmezett az x = 0-ban nem tudjuk használni az "antiderivált" grafikonjának megadásához 0-tól az integrálfüggvényt. Ezért használjuk az integrálfüggvényt egy másik határral az 1-gyel (és a szoftver a negatív x-re is másként kezeli). Most még nem tudjuk hogyan értelmezzük a határozott integrált olyan intervallumon, ahol az integrandus végtelen lesz; ezt a kérdést később még újra megvizsgáljuk. A program numerikus módszereket használ a függvény felrajzolásához, melynél ugyancsak vannak problémák a végtelen miatt.
- Nézzük a 7. példát, amely egy exponenciális függvényt mutat! Tudjuk, hogy az ex függvény deriváltja éppen ex, így kitalálhatjuk, hogy a primitív függvénye az ex-nek éppen ex. Úgy tűnik a grafikonnak helyes az alakja, csak lejjebb van tolva a függőleges tengely menén. Ez azért van , mert az "antiderivált" úgy van ábrázolva mint az integrálfüggvény
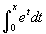, amely zérus x = 0-ban. Így az integrálfüggvény megadja az ex - 1 primitív függvényt. Mivel ezután ehhez az eredményhez még hozzáadjuk a C konstanst és a -1 szintén egy konstans, össze lehet vonni -1-gyet és a C-t csak egyetlen C-be, mivel ez egy tetszőleges kontans. Így a szabály 
.
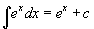- Nézzük a 8. példát, amely a koszinusz függvényt mutatja! Az "antiderivált" úgy néz ki, mint a szinusz függvény, és mivel tudjuk, hogy a sin(x) deriváltja a cos(x), a szabály az "antderivált"-ra
.
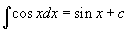- Nézzük a 9. példát, a szinusz függvényt (görgessen le a menü ablakban, hogy megtalája a 9. példát)! Az "aniderivált" úgy néz ki, mint a koszinusz függvény, de meg van fordítva és föl van tolva . Mivel tudjuk, hogy a cos(x) driváltja -sin(x), a -cos(x) deriváltja sin(x), így azt várjuk, hogy a szinusz "antiderivált"-ja úgy néz ki, mint a mínusz koszinusz. Az eltolás a szoftver grafikus ábrázolásából ered az integrálfüggvény
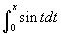használata miatt, így most is az ábrázolt "antiderivált" függvénynek át kell mennie az x tengelyen az origóban. Hasonlóan az exponenciális függvény példájához, elhagyhatjuk a +1 eltolást, mivel ez csak egy konstans hozzáadását jelenti, a szabály tehát: 
.
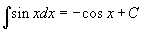- Integrandusnak választhatja saját függvényeit, elsősorban azokat, amelyknek ismerjük a deriváltját. Ki lehet próbálni két függvény összegét, és látni fogja, hogy a határozott inegrál additív tulajdonsága általában is igaz az "antideriváltra" is. Más szavakkal,
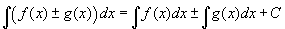. Ha kipróbálja a szorzat, a hányados, és az összetett függvényeket, rájön arra, hogy a deriváltakhoz hasonlóan szükségünk van toábbi összetett szabályokra. Legyen óvatos a függőleges aszimptotákkal , mint például a sec(x)tan(x) függvény (melyről tudjuk, hogy a sec(x) függvény deriváltja, így az "antiderivált" függvénynek sec(x) + C-nek kell lennie). Ha ezt kipróbálja, akkor helyes grafikont kap mindaddig, amíg nem keresztezi az aszimptotát. Amikor a függvény átmegy egy asziomptota helyén, az ábrázoló szoftver összezavarodik, mivel nehézséggel küzd az integrálfüggvény kiértékelésénél, amikor a függvény végtelenbe megy.
This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.