Bevezetés a differenciálegyenletek elméletébe
Tegyük fel, hogy a következő egyenletnek szeretnénk megtalálni a megoldását: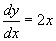 
. Az olyan egyenletet, amely egy függvény deriváltját is tartalmaza differenciálegyenletnek nevezzük, megoldása pedig azt jelenti, hogy megkeressük azt a függvényt, amely kielégíti az egyenletet. Ebben az esetben, y = f (x) = x² + C adja a megoldások családját (a megoldássereget). Amennyiben tudjuk, hogy y = 3, amikor x = 0, akkor azt is tudjuk, hogy y = x² + 3 a speciális megoldás. Ennek az appletnek a segítségével megpróbáljuk felfedezni a legegyszerűbb differenciálegyenletek megoldásának módszereit.
Próbálja a következőket!
- Az első példa a 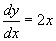egyenlet megoldásának a grafikonját mutatja! A szürke görbe azt a megoldását ábrázolja, amikor a megoldásfüggvénynek egy pontja a (0,0) koordinátájú pont, míg a magenta színu görbe a (0,3) ponton áthaladó függvény megoldást ábrázolja, amely a bevezetőben már említett példa. Változtatni lehet azt a pontot, amely a megoldáshalmaznak egy speciális elemét határozza meg (melyet kezdeti feltételnek hívunk), írja be a számokat az x és az y ablakba, vagy mozgassa a csúszkát, vagy klikkeljen a magenta pontra a grafikonon! Speciálisan vegyük azokat az eseteket, amikor x = 0, és mozgassa az y csúszkát, figyelje mi történik a grafikonon! Azt látja, amit várt? Most nézzük azokat az eseteket amikor y = 0, és mozgassuk az x csúszkát! Mi történik a grafikonnal? Talán azt várta, hogy a görbe jobbra és balra fog mozogni, de tény, hogy a görbe fel és le mozog. Ez azért van, mert a megoldáshalmaz minden eleme egymáshoz képest függőlegesen eltolt parabolákból áll; mozgatva a kezdeti feltétel pontját vízszintesen, felismerhetőek a különböző fügőlegesen eltolt parabolák. Vegyük az x = 1 és y = -1 esetet! Mi a feltétel melletti megoldás? Meg tudjuk határozni, ha behelyettesítjük a koordinátákat az általános megoldásba, ezt kapjuk C-re: -1 = (1)² + C, azaz C = -2. Megjegyzés: a grafikonon az egérrel nem lehet zoomolni, meg kellett akadályozni a véletlenszerű zoomolást, a mozgatható pontra való klikkelés miatt. A képablak mozgatására lehetőség van az egér segítségével (jobb klikk, ha Windows/Linux rendszert használ és option-click Macintosh rendszer esetén).
- Nézzük a 2. példát a legördülő listáról, amely a
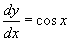egyenlet megoldását mutatja a grafikon! Mozgassa a csúszkát vagy húzza a pontot, hogy megnézze a különböző parikuláris megoldásokat! Ahogyan a fenti példánál tettük, megkapunk egy speciális megoldást egy (x,y) párhoz, ha az adatokat behelyettesítjük az általános megoldásba, y = sin x + C, és megoldjuk C-re.
- Ki tudja próbáli saját példáját, ha a differenciálegyenlet jobb oldalán lévő függvényt változtatja és lenyomja az Enter-t, hogy kirajzoltassa a megoldást! Vegyük észre, hogy a függőleges aszimptoták problémát okoznak, ennek részben az a speciális algoritmus az oka, amit a szoftver használ a rajzoláshoz, de a végtelen, amely az aszimptota következménye, is az okok között van (a későbbiekben többet fogunk erről megtudni)! Megjegyezzük: ha kicsinyíteni szeretne esetleg az látja, hogy a görbe hirtelen eltűnik; ez a megoldás a rajzoló algoritmus eredménye (a görbének ténylegesen meg kellene maradnia).
This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.