Optimalizálás: a maximális térfogat megkeresése
A globális szélsőérték meghatározásának egyik legfontosabb alkalmazása az, amikor valamely mennyiséget optimalizálunk, vagyis megkeressük a minimumát, illetve a maximumát.
Tegyük fel például, hogy egy 25" (inch) hosszúságú és 20" szélességű kartonpapírból szeretnénk készíteni egy felül nyitott dobozt.
Ehhez a papír négy sarkából egyforma négyzeteket kell kivágnunk, majd a papírt úgy kell hajtogatnunk, hogy dobozt formáljon, az alábbi ábrának megfelelően:
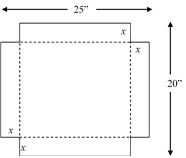
Tegyük fel, hogy azt szeretnénk meghatározni, milyen nagy négyzeteket kell levágnunk, hogy maximális térfogatú dobozt nyerjünk.
Ez az applet bemutatja, hogy hogyan gondolkodjunk a kalkulus segítségével e dobozzal kapcsolatos problémáról.
Próbálja ki a következőket:
- Az applet baloldalán fent a kartonpapír látható, lent pedig egy 3D-s perspektivikus ábra a hajtogatott dobozról.
Az x csúszka mozgatásával állíthat a sarokkivágások méretén. Figyelje meg, hogyan változik a doboz!
Amikor x kicsi, a doboz lapos, keskeny, térfogata csekély. Amikor x nagy, a doboz magas, de megint keskeny és térfogata megint csekély.
Valahol a kettő között lesz a doboz maximális térfogatú. Nyilvánvalóan a legkisebb x érték a nulla,
amikor egyáltalán nincs sarokkivágás. Mi a lehetséges legnagyobb értéke x-nek? Miért?
- A doboz térfogata, mivel egy téglalap alapú hasábról van szó, szélesség szorozva hosszúság szorozva magassággal.
A magasság nem más, mint a levágott sarok nagysága (ez jelen esetben x).
A levágott sarkok miatt a doboz alapjának mind a szélessége, mind a hosszúsága kisebb a kartonpapír méreténél.
Így a térfogatot x függvényeként a V(x) = x(25 - 2x)(20 - 2x) képlet adja meg.
E függvény grafikonja az applet jobboldalán fent látható. Az x csúszka mozgatásával a megfelelő pont végigfut a grafikonon,
és az x értékhez tartozó térfogatérték is megjelenik a grafikon felső sarkában.
- Voltaképpen a kalkulus alkalmazása nélkül is megoldhatnánk a problémát úgy, hogy számológépes ábrázolással megkeressük a grafikon legmagasabb pontját.
Mégis célravezetőbb az, ha a térfogatfüggvényt deriváljuk, egyenlővé tesszük nullával, majd ennek megoldásával
eljutunk a kritikus pontokhoz, melyek közül kiválasztjuk a lokális maximumhelyet, és végül összevetjük az ezen a ponton felvett térfogatot a végpontokban felvett térfogatértékekkel
(a jelen problémánál ez utóbbira nem lesz szükségünk, hiszen a térfogat nulla az x szóba jöhető tartományának két végpontján).
A deriváltat sokunk számára egyszerűbb úgy meghatározni, hogy először elvégezzük a beszorzásokat a térfogatképletben, majd az így nyert
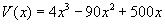függvényt deriváljuk. Az eredmény: 
.
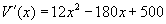Ha ezt egyenlővé tesszük nullával és megoldjuk az egyenletet (a másodfokú megoldóképlettel), a következő két értéket kapjuk:
x ≈ 11.319 és x ≈ 3.681. Az első érték kívül esik az elfogadható
x értékeken, így a második adja a megoldást. Ha az x ≈ 3.681 értéket visszahelyettesítjük
a térfogatképletbe, a maximális térfogatra azt kapjuk, hogy V ≈ 820.529 in³ (köbinch).
Az appletben a deriváltat a jobb alsó grafikon ábrázolja. Figyelje meg, hogy a derivált függvény ezen a ponton metszi az x-tengelyt
és pozitívból negatívba megy át, jelezve, hogy ez a kritikus pont lokális maximumhely!
- Az applet alján lévő két mezőbe beírhatja a kartonpapír hosszát és szélességét (L és W).
Írjon be ide különféle értékeket, hogy lássa, miként befolyásolja ez a megoldást és a térfogatfüggvény alakját!
Figyelje meg, hogy az applet automatikusan kiszámolja a grafikon határpontjait (azaz nem kell nagyítást alkalmaznia)!
Az applet kijelzi a térfogatképletet is (az x, L és W adatokkal), továbbá
a derivált képletét, de a deriváltat algebrai átalakítások nélkül
(azaz a szorzási szabály alkalmazásával) számolja ki, így a derivált képlete kissé kusza lesz.
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.