Összetett függvények deriváltja (láncszabály)
Mi lesz két függvény összetételének a deriváltja?
Próbálja ki a következőket:
- Az első példa egy egyenes és egy parabola összetételét mutatja. Itt f (x) = 2x, g (x) = x2 és h (x) = g (f (x)).
A lila színnel ábrázolt grafikonoknak meghúztuk az érintőit (ami f esetében nehezen kivehető, mivel f maga is egy egyenes).
Az f grafikonján (baloldalon) lát egy (elhúzható) piros négyzetet és egy piros vonalat. A piros vonal hossza
reprezentálja az f x bemenőértékeit és a függőleges zöld vonal reprezentálja az f y kimenőértékeit. Mivel f az összetétel
belső függvénye, így az f zöld y kimenőértékei lesznek a g függvény x bemenőértékei, és a középső grafikonon valóban látni is fog egy vízszintes zöld vonalat,
mely g x bemenőértékeit mutatja (ennek a két zöld vonalszakasznak a hossza azonossá válik, ha a koordinátatengelyek beosztását egyformára állítja).
A g grafikonján ugyancsak lát egy függőleges kék vonalat, mely g y kimeneteleit reprezentálja.
A jobboldali grafikon mutatja az összetételt. Itt az x bemenet azonos az f eredeti piros bemenetével, a kimenet pedig a g kék kimenetével.
Kattintson az "Equalize Axes" gombra, majd húzza el a csúszkát! Figyelje meg, hogyan jelenítik meg a színes vonalszakaszok az összetétel folyamatát!
A példán figyelje meg azt is, hogy az érintő meredeksége fel van tüntetve mindegyik grafikon jobb felső sarkában!
Milyen kapcsolatot vesz észre az f és a g görbékhez húzott érintők meredekségei és az összetett függvényhez húzott érintő meredeksége között?
Húzza el a csúszkát, és nézze meg, hogy beválik-e a sejtése!
- Válassza ki a második példát a legördülő menüből! Most g egy exponenciális függvény.
Érvényes-e még a meredekségekre az a kapcsolat, amit az előbb megfigyelt? Vizsgáljon meg néhány további példát a legördülő menüből,
ahol különféle f és g függvényeket talál!
- Minden bizonnyal kitalálta már, hogy az összetett függvény érintőjének a meredeksége a két másik meredekség szorzata.
Az első grafikonon az érintő meredeksége f '(x), ám figyelje meg, hogy a középső grafikonon a meredekséget egy másik helyen számoljuk ki
(azaz nem az x helyen, hanem az y = f (x) helyen). A középső grafikonon a meredekség g ' (f (x)).
Ha e kettőt összeszorzza, megkapja az összetett függvény deriváltjának az általános formuláját, melyet láncszabálynak is nevezünk:
.
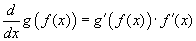E szabály szerint tehát a külső függvény deriváltját (a belső függvényt nem bolygatva) összeszorozzuk a belső függvény deriváltjával.
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.