Függvények szorzatának és hányadosának a deriváltja
Mi lesz két függvény szorzatának a deriváltja? És a hányadosuké?
Az előző lapon láttuk, hogy az összeg és a különbség szabályai igen egyszerűek, ám a szorzat és a hányados szabályai bonyolultabbnak tűnnek.
Próbálja ki a következőket:
- Az első példa egy összeget mutat. A baloldali panel az f (x) függvény grafikonját mutatja lilával, a deriváltját pedig kékkel.
A középső panel a g (x) grafikonját és deriváltját mutatja. A jobboldali panel h (x) grafikonját és deriváltját mutatja,
ahol h (x) jelen esetben f és g összege. Először is nézzük meg a függvények grafikonjait (a lila görbéket)!
Példánkban f egy szinuszgörbe, g egy egyenes és h az összegük, mely ugyanúgy tekergőzik, mint a szinuszgörbe.
Azután nézzük meg a kék deriváltgörbéket! A szinusz deriváltja koszinusz, az egyenes deriváltja egy vízszintes egyenes,
az összegük deriváltja pedig e kettő összege (vagyis egy fölfelé eltolt koszinuszgörbe).
- Válassza ki a második példát a legördülő menüből. Itt f és g ugyanaz, de h most a szorzatfüggvény.
Nyilvánvaló, hogy h deriváltja nem egyenlő f és g deriváltjainak a szorzatával (ha az volna, egy elnyújtott koszinuszgörbére hasonlítana).
A szorzásra vonatkozó szabály a következő:
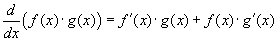. Más szóval
két függvény szorzatának a deriváltja egyenlő az első függvény derivált szorozva a második függvénnyel, plusz az első függvény szorozva a második függvény deriváltjával.
- Válassza ki a harmadik példát, mely egy hányadost mutat! A szabály itt a következő:
.
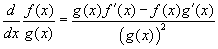Ismerek egy formulát, amellyel könnyebben megjegyezheti ezt. Ha a felső függvényt HI-nek, az alsót pedig HO-nak becézzük, a deriváltjaikat pedig dHI-nek és dHO-nak, a szabály így hangzik: 
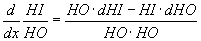, amit úgy olvashatunk ki, hogy "HO dHI minusz HI dHO a HOHÓ-n."
Néha a HIdHO szabályként emlegetik ezt (idézzük fel Cab Calloway-t, amint Mikulásnak öltözve azt énekli, hogy Hi De Ho...).
- Bátran írjon be saját függvényképleteket f és g helyére, hogy megismerje, hogyan néz ki a szorzatuk, hányadosuk, és ezek deriváltjai!
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.