Függvénytranszformációk deriváltja
Legyen f (x) egy tetszőleges függvény és legyen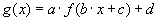 
egy másik függvény,
mely az f transzformáltja. Ebben az appletben azt nézzük meg, hogy milyen kapcsolat van f és g deriváltjai között.
Próbálja ki a következőket:
- Az applet elsőként egy köbfüggvény grafikonját mutatja. A függvényt és a deriváltját lilával jelöljük,
a transzformált függvényt és a deriváltját kékkel. Most csupán a kéket látja, mivel a kiindulásnál a kettő megegyezik.
Tolja el először is a d csúszkát! Mi történik a függvény grafikonjával? Mi történik a deriválttal? Miért?
A d érték változtatásával f grafikonja föl-le tolódik, viszont a görbe meredeksége sehol sem változik.
Ezért g deriváltja azonos lesz f deriváltjával.
- Állítsa most vissza d-t nullára, és tologassa a c csúszkát! Mi történik a függvény grafikonjával? Mi történik a deriválttal? Miért?
A c érték változtatásával a grafikon jobbra-balra tolódik, és a derivált is így tesz.
Ugyanígy, bármikor állíthat az x csúszkán is, mely az érintési pontot tolja el.
- Állítsa vissza c értékét nullára, majd tolja el az a csúszkát!
Mi történik a függvény grafikonjával? Mi történik a deriválttal? Miért? Az a érték változtatásával
a grafikon függőleges irányban megnyúlik vagy összelapul. Amikor megnyúlik, a meredeksége megnő, így a deriváltja is megnyúlik függőleges irányban.
Amikor összelapul, a meredeksége lecsökken, így a deriváltja is ellaposodik függőleges irányban. Például
állítsa be az x = 2 és a = 2 értékeket: milyen kapcsolat van a jobboldali grafikonon kijelzett
deriváltértékek között? Állítsa be az a = 3 értéket, stb.
Bizonyára észrevette, hogy a transzformált függvény deriváltja pontosan a-szorosa lesz az eredeti függvény deriváltjának.
- Állítsa vissza a értékét 1-re, majd tolja el a b csúszkát! Mi történik a függvény grafikonjával? Mi történik a deriválttal? Miért?
A b érték változtatásával a grafikon vízszintes irányban megnyúlik vagy összelapul.
A vízszintes megnyúlással a görbe meredeksége lecsökken (azaz nullához tart), így a deriváltja ellaposodik.
A vízszintes összelapulással a görbe meredeksége megnő (azaz nullától távolodik), így a deriváltja függőleges irányban megnyúlik.
Ám ha megnézi a deriváltértékeket, azok viselkedése ennél némileg bonyolultabbnak tűnik. Állítsa be például az x = 2 és b = 2 értékeket!
A transzformált függvény deriváltjának az értéke nyilvánvalóan nem áll olyan egyszerű kapcsolatban az eredeti függvényértékkel, mint az a esetében.
- Válassza ki a második példát, egy szinuszgörbét, és kísérletezzen a csúszkákkal!
Nézze meg például, hogy az a = 1, c = d = 0 beállítás mellett mi történik a b csúszka tologatásakor!
E példánál még szembetűnőbb, hogy a transzformált függvény deriváltja mind függőlegesen, mind vízszintesen megnyúlik, illetve összelapul.
- Minderre rájöhet úgy is, ha a g(x) függvényt a láncszabály alkalmazásával deriválja:
.
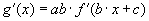Figyelje meg, hogy a deriválás során a d érték eltűnt, vagyis a függőleges eltolás nem befolyásolja a deriváltat!
A c érték ugyanazon a helyen maradt, vagyis a vízszintes eltolás eltolja a deriváltat is.
Az a érték is ugyanazon a helyen maradt, vagyis a függőleges nyújtás/lapítás ugyanígy megnyújtja/ellapítja a deriváltat is.
Figyelje meg, hogy a b érték két helyen jelenik meg a képletben, ami azt jelenti, hogy az érték változása hatással van a derivált
függőleges és vízszintes irányú megnyúlására, illetve összelapulására is!
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.