Kalkulus Appletek

Összehasonlító kritérium

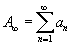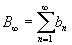Az összehasonlító kritérium használatakor ismert konvergens sor segítségével döntjük el egy új sor konvergenciáját. Tegyük fel, hogy van két sorunk: és , ahol 0 ≤ a_n < b_n. Amennyiben B konverens, akkor A is az lesz. Ugyancsak igaz, ha A divergens, akkor B is az lesz. Ha sejtjük, hogy az A konvergens, megpróbálhatunk keresni egy hasonló B sort, amelynek minden tagja nagyobb, mint az A sor tagjai és a B sorról tudjuk, hogy konvergens, így biztosítja azt , hogy A konvergens. Ezt a logikát követve, ha van egy B sor, amelyről sejtjük, hogy divergens lesz, akkor kereshetünk egy hasonló A sort, amelynek a tagjai mind kisebbek a B sor megfelelő tagjainál, valamint az A sorról tudjuk, hogy divergens, akkor biztosak lehetünk abban, hogy B is divergens.

Próbálja ki a következőt:

1. Az applet a követkző sort mutaja 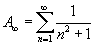. Ez hasoló a p-sorhoz, ezért látható a p-sor is, mint B sor. A kék pontok az A sor részletösszegeit és a kék/lila téglalapok a sorozat a_n elemeit ábrázolják. A piros pontok jelölik a B sor részletösszegeit és a piros/rózsaszín téglalapok a b_n elemeket. Megjegyezzük, hogy minden a_n kisebb, mint a megfelelő b_n és mind pozitív, tehát alkalmazhatjuk az összehasonlító kritériumot. Tujuk, hogy a p-sor p > 1 esetén konvergens, B konvergens, és így A is az. A táblázat a jobb felső sarokban az A és B esetre is azt támasztja alá, hogy mindkettő sor konvergens.
   
   
2. Nézzük a 2. példát a legördülő listáról, amely a következő sort mutatja: 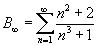! Ez hasonlít a harmonikus sorhoz, amit A sorként ábrázolunk. Minden b_n nagyobb, mint a megfelelő a_n tagok, és mind pozitív, így alkalmazhatjuk az összehasonlító kritériumot. Mivel a harmonikus sor divergens, ezért B is divergens. A táblázat értékei alapján nem teljesen világos, hogy B konvergens vagy divergens, így az összehasonlító kritérium hasznos ennek meghatározásához.

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.