Kalkulus Appletek

Határérték összehasonlító teszt

A határérték összehasonlító teszt hasonló az összehasonlító kritériumhoz abban az értelemben, hogy egy másik sort használunk annak eldöntésére, hogy konvergens vagy divergens a vizsgálni kívánt sor. Tegyük fel, hogy két sorunk van: és , ahol a_n >0 és b_n > 0. Ha (azaz, ha az általános tagok hányadosa egy számhoz konvergál, miközben n tart a végtelenhez), akkor mindkét sor vagy konvergens, vagy divergens. Amannyiben B sorként egy megfelelő, ismert sort választunk (általában a p-sort szoták választani), akkor használva a tesztet eldönthetjük, hogy A konvergens vagy nem.

Próbálja ki a következőket!

1. Az applet a következő sort ábrázolja: . Egy hasznos út ahhoz, hogy racionális tört esetén megkeressük az összehasonlításhoz szükséges sort, ha a vizsgálandó sor számlálójában lévő legnagyobb hatványkitevőjű n-et elosztjuk a nevezőben lévő legnagyobb hatványkitevőjű n elemmel, esetünkben ez . A táblázat az a_n/b_n arányokat mutatja, amely alapján úgy tűnik a hányados 1-hez konvergál. Ezt meg tudjuk erősíteni: . 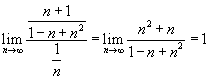A határérték összehasonlító teszt szerint tehát vagy mindkettő konvergens vagy mindkettő divergens. Mivel tudjuk, hogy a harmonikus sor diergens, A -nak is divergensnek kell lennie.
   
   
2. Nézzük a 2. példát a legördülő listáról, amely a sort mutatja. Használjuk az előző példánál bevezetett módszert az összehasonlító sor keresésére, csak most az exponenciális tagot is vegyük bele: ! A hányados határértéke láthatóan 1-hez konvergál (az "undefined" a táblázatban annak a következménye, hogy b tagjai olyan kicsivé válnak, hogy az algoritmus úgy tekinti, mintha 0-val osztott volna), ezt meg tudjuk erősíteni: . 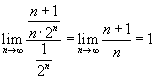A határérték összehasonlító teszt szerint ebben az esetben vagy mindkét sor konvergens vagy mindkét sor divergens. Mivel , a B sor mértani sor, amelynél r = 1/2, így tudjuk, hogy konvergens, tehát A szintén konvergnes.

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.