Kalkulus Appletek

Integrálkritérium

Az integrálkritérium egy másik lehetőség arra, hogy ellenőrizük a végtelen számsor konvergens vagy divergens voltát. Tegyük fel, hogy olyan sorozatunk van, amelyhez az általános elem az a_n = f (n) alapján van értelmezve, ahol f egy függvény. Azt szeretnénk tudni, hogy a 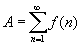sor konvergens vagy divergens. Ha az f függvény pozitív, monoton csökkenő és folytonos minden x > c, és az 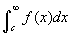konvergens, akkor a sor is konvergens lesz, és ha az integrál divergens, akkor a sor is az lesz. Tehát, ha az f függvényt tudjuk integrálni és találunk olyan c -t amelyre f pozitív, monoton csökkenő és folytonos minden x > c-re, akkor alkalmazhatjuk a kritériumot. c = 1 a leginkább választott c, de ez függ a konkrét függvénytől, lehet nagyobbat is választani c értékének.

Próbálja ki a következőket!

1. Az első példa a harmonikus sort mutatja. A grafikon az f (x) = 1/x függvény görbéje kékkel van megrajzolva. Mivel ez pozitív, csökkevő és folytonos, használhatjuk az integrálkritériumot. Az integrált a következő módon írjuk fel: 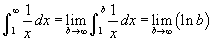. Mivel az ln x függvény minden határon túl nő, ez a határérték nem létezik, így a harmonikus sor divergens.
   
   
2. Nézzük a 2. példát, ahol a sor 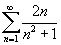! A táblázat és a grafikon szemlélésével nem tudjuk eldönteni a sorról, hogy konvergens vagy divergens. A kék vonallal jelölt függvény pozitív és monoton csökken x > 1 esetén, így használhatjuk az integráltesztet: 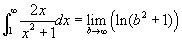, a megoldáshoz a következő helyettesítést használtuk: u = x² + 1. Világos, hogy a határérték nem létezik, tehát a sor divergens.
   
   
3. Nézzük a 3. példát, amely a következő sort mutatja 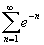! A gafikonról és a táblázatból látható, hogy a sor konvergens, de ezt meg kell erősítenünk az integrálteszttel. Mivel az e^-x függvényt könnyű integrálni, pozitív, monoton csökkenő és folytonos minden x-re, tehát használhatjuk az integralkritériumot: 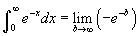. Mivel ez a határérték zérus, az exponensben megjelenő negatív előjel miatt, a sor konvergens. Megjegyezzük, hogy az 1 helyett kisebb alsó határt, 0 értéket választottunk az integrál alsó határának, azért, hogy az integrál megadását kicsit könyebbé tegyük.

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.