Függvények konstansszorosának deriváltja
Mi történik egy függvény deriváltjával, ha a függvényt megszorozzuk egy konstanssal?
Próbálja ki a következőket:
- A példa az f (x) = kx egyenest mutatja. Tudjuk, hogy az f (x) = x egyenes meredeksége pontosan 1.
Mit csinál a k a meredekséggel? Tologassa a k csúszkát és figyelje meg, hogy az új meredekség pontosan k!
- Válassza ki a második példát, mely egy parabola k-szorosát mutatja! Ha k > 1, mi történik a parabola meredekségével? Tologassa a k csúszkát és olvassa le a választ!
Mi történik a deriválttal? Állítsa be az x = 1 és k = 1 értékeket, és nézze meg, mennyi f '(1) értéke. Most állítsa a k-t 2-re:
mi történik az x = 1 pontbeli deriválttal? Állítsa k-t egy másik értékre, és nézze meg, felfedez-e valamilyen szabályszerűséget a derivált viselkedésében!
- Válassza ki a harmadik példát, mely egy szinuszgörbe konstansszorosát mutatja! A k változtatása mit eredményez a deriváltnál?
- Bizonyára rájött, hogy egy függvény konstansszorosának a deriváltja nem más, mint a függvény deriváltjának a konstansszorosa, azaz:
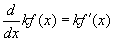 .
.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
