Függvények összegének és különbségének a deriváltja
Mi a deriváltja két függvény összegének? És a különbségének? Ezen az oldalon ezeket a kérdéseket tisztázzuk az alábbi applet segítségével,
melyről elhagytuk a határpont-szerkesztő panelt, hogy
legyen elég hely mindhárom grafikon számára (a Zoom gombok viszont megmaradtak).
Próbálja ki a következőket:
- A példa három grafikont mutat: f (x) = x, g (x) = x2, és h (x) = f (x) + g (x).
Az egyes grafikonokon az érintők is fel vannak tüntetve, és pozíciójukat az x csúszka szabályozza. Mindegyik grafikon alján fel van tüntetve az aktuális x pozícióhoz tartozó függvényérték.
Leolvashatjuk, hogy a h (x) értéke pontosan megegyezik az f (x) és a g (x) függvényértékek összegével,
amit az f és a g értékek összeadásával ellenőrizhetsz. Mindegyik grafikon jobb felső sarkában jelezzük az érintő meredekségét (slope =).
Az f érintőjének meredeksége konstans, mivel f egy egyenes, viszont g meredeksége változik az x változtatásával.
Vajon mekkora lesz h érintőjének a meredeksége? Hogyan függ össze ez a meredekség f és g meredekségeivel?
- Válassza ki a második példát, mely egy parabolát és egy szinuszgörbét mutat! Milyen összefüggés van h érintőjének meredeksége valamint f és g meredekségei között?
Láthatólag h meredeksége pontosan f és g meredekségeinek az összegével egyenlő.
Kipróbálhat más példákat is, ha más képleteket ír be f és g mezőkbe. Létrehozhatja a saját grafikonját is, a "Use Mouse" gombok valamelyikére (vagy mindkettőre) rákattintva.
A grafikon ekkor egy egyenest mutat néhány rácsponttal tarkítva. Ha kattintással elhúz egy ilyen pontot, a függvény alakja ott megváltozik.
Föl-le tologathatja őket, s így egészen tekervényes görbéket tud létrehozni! Most tolja el a csúszkát és nézze meg, hogy h meredeksége még mindig f és g meredekségeinek az összege-e!
Az általános szabály a következő:
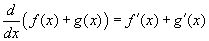. Más szóval,
az összeg deriváltja a deriváltak összegével egyenlő.
- Válassza ki a harmadik példát! Ez hasonló az előzőhöz, csak most h f és g különbségével egyenlő. Milyen összefüggés van h érintőjének meredeksége valamint
f és g meredeksége között? A csúszkával játszadozva, illetve néhány saját képletet beírva az f és g mezőkbe minden bizonnyal rájön arra, hogy
a különbség deriváltja megegyezik a deriváltak különbségével, vagyis
.
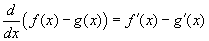- Válassza ki a negyedik példát, mely f és g függvények szorzatát mutatja! Vajon igaz-e az, hogy h meredeksége megegyezik f és g meredekségeinek szorzatával?
Úgy tűnik, nem igaz. Például különösen nagy eltérést tapasztalhat az x = 0.5 értéknél. Itt f meredeksége 1, ám h meredeksége nem azonos g meredekségével!
Vagyis a szorzat deriváltja nem egyenlő a deriváltak szorzatával, hanem komplexebb összefüggés van közöttük (mint majd később látni fogjuk).
Ha a h függvény képletét most átírja a f (x) / g (x) képletre, hamar be fogja látni azt is, hogy
két függvény hányadosának a deriváltját ugyancsak nem a deriváltak hányadosa fogja megadni. Végezetül írja be a h (x) = f (g (x)) képletet és járja körül ezt az esetet is!
Azt fogja találni, hogy a függvények kompozíciója ugyancsak bonyolultabb eset az összegnél és a különbségnél.
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.