Trigonometrikus függvények
Ezen az oldalon a trigonometrikus függvények deriváltjait vizsgáljuk meg. A kalkulusban rendszerint radiánokban számolunk fokok helyett.
Próbálja ki a következőket:
- Az első példa a szinusz függvényt mutatja. Felismeri a deriváltját? Eszerint
.
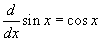Húzza el az x csúszkát, hogy meggyőződjön róla, a derivált függvény valóban bármely adott pontban az érintő meredekségét mutatja!
- Válassza ki a második példát a legördülő menüből! Ez a koszinusz függvény. Mihez hasonlít a deriváltja? Csakugyan:
.
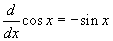Mindkét deriválási formula kifejezhető lenne csak a szinusszal, hiszen a szinusz és a koszinusz függvények vízszintes eltolással átvihetők egymásba.
Mindazonáltal a bevett gyakorlathoz ragaszkodva a fent mutatott módon adjuk meg a deriváltakat.
- Válassza ki a harmadik példát, a tangens függvényt! Most távolról sem nyilvánvaló, hogy mi a derivált, de nagyjából úgy néz ki, mint a szekáns függvény, azzal a különbséggel, hogy jelen esetben
az összes görbe az x-tengely fölött helyezkedik el. A tangens deriválálási szabálya:
.
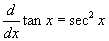- Válassza ki a negyedik példát, mely a szekáns függvényt mutatja! A deriváltja nagyjából úgy néz ki, mint a tangens, de mégis más. A deriválási szabálya:
.
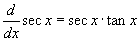Ezt a két deriváltat a következőképpen jegyezhetjük meg: a tan x vagy a sec x deriváltja megegyezik a másik függvény sec x-szorosával. Vagyis a tan x deriváltja sec x-szer sec x
(most a sec x a "másik függvény"). A sec x deriváltja pedig sec x-szer tan x (most ez utóbbi a "másik függvény").
- Válassza ki az ötödik példát, a kotangens függvényt! A deriváltja hasonlít a tangens deriváltjához, csak épp fejjel lefele áll. A deriválási szabálya:
.
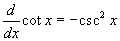Figyelje meg, hogy ez nagyon hasonlít a tan x deriválási szabályára, csak most a sec x helyén csc x áll negatív előjellel.
- Válassza ki a hatodik példát, a koszekáns függvényt! A deriválási szabálya:
.
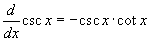Ez hasonló a sec x szabályához, csak most a képletben csc x és cot x áll, továbbá kapott egy negatív előjelet.
Figyelje meg, hogy az összes ko-függvény (koszinusz, kotangens, koszekáns) deriváltja negatív előjelű, míg a másik három (szinusz, tangens, szekáns) deriváltjainak nincs negatív előjele!
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.