Függvénygörbe vizsgálata: alapok
A differenciálszámítás egyik alkalmazása a függvénygörbék viselkedésének elemzése.
Ebben az appletben a görbékkel kapcsolatos alapvető tulajdonságokat és alapfogalmakat tekintjük át.
Próbálja ki a következőket:
- Az első példa az
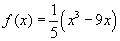köbfüggvényt mutatja
a baloldali grafikonon. Hol növekszik ez a függvény? Egy függvényről azt mondjuk, hogy növekszik
egy zárt intervallumon, ha az intervallumon belüli bármely a és b pontpárra teljesül az, hogy ha a > b, akkor f (a) > f (b).
Más szóval, ha balról jobbra végighalad a grafikonon, "hegynek fel" kell mennie.
A csökkenést teljesen hasonlóan definiáljuk. Mindezt kiolvashatjuk a deriváltból is
(a középső grafikonon), hiszen amikor egy függvény növekvő, a derivált pozitív, amikor pedig csökkenő, a derivált negatív.
Mozgassa a csúszkát és figyelje az érintő meredekségét a jobboldali grafikonon. Amikor a meredekség pozitív,
a függvény növekszik és a derivált pozitív. Amikor a meredekség negatív, a függvény csökkenő és a derivált negatív.
A függvényünk növekszik a (-∞; -3^(1/2)] és [3^(1/2); ∞) intervallumon. Ezt így is írhatjuk: -∞ < x ≤ -3^(1/2) és 3^(1/2) ≤ x < ∞.
A függvényünk csökkenő a [-3^(1/2); 3^(1/2)] zárt intervallumon.
- Mi a helyzet a görbe azon pontjaival, ahol a görbe deriváltja nulla?
Egy függvény értelmezési tartományának azt a pontját, ahol az első derivált nulla vagy meghatározatlan kritikus pontnak fogjuk nevezni.
A grafikonunkon két kritikus pont van, az x = -3^(1/2) és az x = 3^(1/2).
- A kritikus pontok közül kerülhetnek ki a lokális szélsőértékek (szokták relatív szélsőértéknek is nevezni).
Az f (x) függvénynek lokális minimuma van az x = c helyen, ha
f (c) kisebb-egyenlő a c környezetében felvett f függvényértékeknél.
A lokális maximumot teljesen hasonlóan definiáljuk.
Mint látjuk, a függvényünknek x = -3^(1/2) helyen lokális maximuma, az x = 3^(1/2) helyen lokális minimuma van.
Ezt úgy is meghatározhatjuk, hogy az első derivált teszttel megkeressük a függvény kritikus pontjait
(ahol tehát az első derivált nulla vagy meghatározatlan), majd ezután megvizsgáljuk, hogy a derivált előjelet vált-e.
Figyelje meg, hogy az x = -3^(1/2) pontban az első derivált értéke nulla és (balról jobbra haladva) pozitívról negatívra vált.
Ez azt jelenti, hogy az x = -3^(1/2) pont lokális maximumhely. Az x = 3^(1/2) pontban a derivált szintén nulla,
ám itt a derivált előjele negatívról pozitívra vált, így az x = 3^(1/2) pont lokális minimumhely.
Azt a pontot, ami maximum vagy minimum szélsőértéknek nevezzük,
ha több ilyen pont van, maximumoknak, minimumoknak, illetve szélsőértékeknek nevezzük.
- A konvexitás azt írja le, hogy miként görbül a függvénygörbe. Az f függvény konvex egy nyílt intervallumon, ha
f ' növekszik, és konkáv, ha f ' csökken.
Ez egyben azt is jelenti, hogy a függvény konvex, ha f '' (a második derivált) pozitív, és konkáv, ha a második derivált negatív.
Inflexiós pontnak nevezzük azt a pontot, ahol a függvénynek létezik érintője és konvexről konkávra, vagy konkávról konvexre vált.
A példánkban a függvényünk konkáv a (-∞; 0) intervallumon és konvex a (0; ∞) intervallumon.
Inflexiós pontja van a nullában. Figyelje meg, hogy a konvexitást leolvashatjuk a második derivált grafikonjáról
(a jobboldali grafikonról). Ahol a függvény konvex, ott a második derivált pozitív, ahol pedig konkáv, ott a második derivált negatív,
és végül ahol a második derivált nulla, ott inflexiós pont van.
- A második derivált hasznos lehet annak eldöntésénél is, hogy egy kritikus pont vajon maximum vagy minimum-e.
Az x = -3^(1/2) pontban a második derivált negatív, vagyis a függvény konkáv. Ezért ez a pont lokális maximum (azaz egy konkáv púpnak a teteje).
Az x = 3^(1/2) pontban a második derivált pozitív, vagyis a függvény konvex. Ezért ez a pont lokális minimum (azaz egy konvex völgynek az alja).
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.