Lagrange-féle középértéktétel
A középértéktétel azt állítja, hogy ha egy f függvény folytonos egy a ≤ x ≤ b intervallumon és differenciálható az a < x < b intervallumon, akkor
létezik egy olyan a < c < b szám, melyre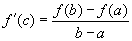 
.
Ez azt jelenti, hogy létezik valahol az intervalumban egy olyan hely, ahol a görbe meredeksége megegyezik az intervallumon vett átlagos meredekséggel
(vagy ami ugyanaz, az (a, f (a)) és a (b, f (b)) pontokon átmenő szelő meredekségével).
Próbálja ki a következőket:
- Az applet első példája egy parabola grafikonját mutatja. A piros pötty koordinátái (a, f (a)), a kék pöttyé (b, f (b)), a lila pöttyé pedig (c, f (c)).
A grafikon mutatja az (a, f (a)) és (b, f (b)) pontokat összekötő szelőt és annak meredekségét is. A középértéktétel szerint létezik egy olyan a és b közötti c érték, hogy f meredeksége c-ben
megegyezik a szelő meredekségével. Tologassa a c csúszkát, amíg nem talál olyan pontot, amelyre teljesül ez (ennél a pontnál azt látja majd, hogy az érintő párhuzamos a szelővel)!
Ha az a és b csúszkát tologatja, megváltozik a szelő meredeksége, így ehhez egy új c pontot kell találnia.
- Válassza ki a második példát a legördülő menüből, mely egy szinuszgörbét mutat! Tolja el a c csúszkát, hogy egy olyan helyet találjon, ahol a meredekségek egyenlők!
Több ilyet is talál? A középértéktétel csupán annyit állít, hogy legalább egy ilyen c érték létezik, ám létezhet egynél több is.
- Válassza ki a harmadik példát, mely az abszolútérték függvényt mutatja! Ez a függvény az a és b között egy ponton nem differenciálható.
Tolja el a c csúszkát: egyformává tudja tenni a meredekségeket? Nem. Pontosan emiatt követeli meg a középértéktétel, hogy a függvény differenciálható legyen az intervallumon.
- Válassza ki a negyedik példát, mely egy szakadásos függvényt mutat! Tologassa a c csúszkát: egyformává tudja tenni a meredekségeket? Nem. Pontosan emiatt követeli meg a középértéktétel, hogy a függvény folytonos legyen az intervallumon.
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.