A derivált függvény
Definiáltuk, hogy mit jelent a derivált egy pontban. Ha vesszük a függvény minden pontjában a pontbeli deriváltat,
ezzel voltaképpen egy új függvényt kapunk.
Ez a derivált függvény az eredeti függvény bármely pontjához tartozó derivált értékét fogja feltüntetni.
A derivált függvényt így definiáljuk:
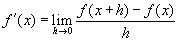
A definíció egy függvényt ad meg. Ha a derivált függvény értékét kiszámoljuk egy adott
x pontban, egy olyan számot kapunk, mely maga a pontbeli derivált lesz (azaz az f változásának mértéke,
vagyis az f grafikonjának a meredeksége). Ha y = f (x), a derivált függvényt így is jelölhetjük: 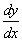 . Ez a különbségi hányadosra emlékeztet, hiszen azt fejezi ki, hogy "mekkora y változás esik az x változásra."
Egy harmadik jelölés a
. Ez a különbségi hányadosra emlékeztet, hiszen azt fejezi ki, hogy "mekkora y változás esik az x változásra."
Egy harmadik jelölés a 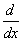 kifejezéssel jelöli a deriválás műveletét:
kifejezéssel jelöli a deriválás műveletét: 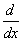 f (x).
Ez a művelet különbözik a megszokott + és - algebrai műveletektől, melyek számokra vonatkoznak és számokat adnak eredményül. A
f (x).
Ez a művelet különbözik a megszokott + és - algebrai műveletektől, melyek számokra vonatkoznak és számokat adnak eredményül. A 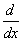 művelet függvényekre vonatkozik és új függvényeket
(derivált függvényeket) ad eredményül. Amikor kiszámoljuk a derivált függvény értékét egy adott pontban,
például az x = 2 pontban, használjuk az f ' (2) vagy
művelet függvényekre vonatkozik és új függvényeket
(derivált függvényeket) ad eredményül. Amikor kiszámoljuk a derivált függvény értékét egy adott pontban,
például az x = 2 pontban, használjuk az f ' (2) vagy 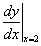 jelöléseket is.
jelöléseket is.
Próbálja ki a következőket:
- Az első applet egy parabolát mutat a baloldalon, és a parabola derivált függvényét a jobboldalon.
Az applet alján található egy csúszka, mellyel beállíthatja az x koordinátát, melynek értéke megjelenik a csúszka melletti
mezőben. A baloldali grafikonon van egy piros egyenes, mely az x koordinátához tartozó
érintőt ábrázolja. Mozgassa a csúszkát és figyelje meg, hogy az érintő úgy mozog, hogy mindig a csúszkával beállított
x koordinátához tartozó érintőt mutatja! A függvénygrafikon bal alsó sarkában lévő mező az f (x) függvényértékeket mutatja.
- Most nézzük meg a jobboldali grafikont, mely az f
' (x) derivált függvényt mutatja! Először is nézze meg a piros érintőt: mennyi a meredeksége?
A meredekségnek az adott x koordinátához tartozó deriváltnak kell lennie,
vagyis ugyanannak az értéknek, mint amit a derivált függvény ezen az x koordinátájú helyen felvesz.
A meredekséget a derivált grafikonjának bal alsó sarkában lévő kijelző mutatja.
A derivált függvény grafikonjának a pontját egy piros célkereszt is jelzi.
- Kattintson rá az "x=" mezőre, és írjon az ott lévő érték helyére 0-t!
Most húzza el a csúszkát jobbra! Figyelje meg, hogy ahogyan a piros érintő meredeksége növekszik,
úgy növekszik a derivált függvényértéke is! Most húzza el a csúszkát balra a nullán túl!
Figyelje meg, hogy ahogyan a piros érintő meredeksége egyre negatívabb, úgy lesznek egyre kisebb negatív számok
a derivált függvényértékek! A derivált függvény bármely adott x pontban az f változásának mértékét,
vagy ami ugyanaz, az f grafikonjának a meredekségét fejezi ki.
- Amikor a derivált pozitív, a függvény növekszik. Amikor a derivált negatív, a függvény csökken.
A derivált így az eredeti függvényről nyújt információt. Mi van akkor, ha a derivált 0?
Hol lát ilyet a példában? Miért 0 a derivált ebben a pontban?
- Figyelje meg azt is, hogy a derivált függvény egy egyenesnek tűnik! Ön szerint mindig ez a helyzet, vagy csupán a
parabola sajátosságaiból következik ez?
- Válassza ki a második példát a legördülő menüből, mely egy szinuszfüggvény!
Hogyan néz ki a derivált függvénye? Húzza el a csúszkát, figyelje a piros érintő meredekségét,
és nézze meg, hogy tud-e valamilyen kapcsolatot teremteni az érintő meredeksége és a derivált függvényértéke között!
Van olyan pont, ahol a derivált 0? Mi jellemzi ezeket a pontokat?
- Válassza ki a harmadik példát, mely egy exponenciális függvényt mutat! Hogyan néz ki a derivált függvénye? Húzza el a csúszkát, figyelje a piros érintő meredekségét,
és nézze meg, hogy tud-e valamilyen kapcsolatot teremteni az érintő meredeksége és a derivált függvényértéke között!
Figyelje meg, hogy az exponenciális függvénynél a derivált függvény sehol nem negatív (más szóval
a jobboldali grafikon sohasem megy az x-tengely alá)! Miért? Mit jelent az exponenciális függvény grafikonjára nézve
az, hogy a derivált sehol nem negatív?
- Válassza ki a negyedik példát, mely egy hiperbolát mutat! Hogyan néz ki a derivált függvénye?
Húzza el a csúszkát, figyelje a piros érintő meredekségét,
és nézze meg, hogy tud-e valamilyen kapcsolatot teremteni az érintő meredeksége és a derivált függvényértéke között!
Figyelje meg, hogy ennél a hiperbolánál a derivált függvény sehol sem pozitív (más szóval
a jobboldali grafikon sohasem emelkedik az x-tengely fölé)! Miért? Mit jelent a hiperbola grafikonjára nézve
az, hogy a derivált sehol sem pozitív?
- Mi történik a hiperbolával az x = 0 pontban? Miért meghatározatlan a derivált?
Mennyi az érintő meredeksége (és van itt érintő)?
- Ön is megadhat tetszőleges függvényt, a "f(x)=" mezőbe beírva a képletét, hogy megvizsgálja, hogyan fest
a deriváltja.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
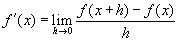
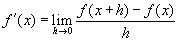
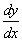 . Ez a különbségi hányadosra emlékeztet, hiszen azt fejezi ki, hogy "mekkora y változás esik az x változásra."
Egy harmadik jelölés a
. Ez a különbségi hányadosra emlékeztet, hiszen azt fejezi ki, hogy "mekkora y változás esik az x változásra."
Egy harmadik jelölés a 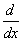 kifejezéssel jelöli a deriválás műveletét:
kifejezéssel jelöli a deriválás műveletét: 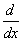 f (x).
Ez a művelet különbözik a megszokott + és - algebrai műveletektől, melyek számokra vonatkoznak és számokat adnak eredményül. A
f (x).
Ez a művelet különbözik a megszokott + és - algebrai műveletektől, melyek számokra vonatkoznak és számokat adnak eredményül. A 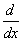 művelet függvényekre vonatkozik és új függvényeket
(derivált függvényeket) ad eredményül. Amikor kiszámoljuk a derivált függvény értékét egy adott pontban,
például az x = 2 pontban, használjuk az f ' (2) vagy
művelet függvényekre vonatkozik és új függvényeket
(derivált függvényeket) ad eredményül. Amikor kiszámoljuk a derivált függvény értékét egy adott pontban,
például az x = 2 pontban, használjuk az f ' (2) vagy 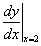 jelöléseket is.
jelöléseket is.