Pontbeli derivált
Az átlagsebesség fogalmát kiterjeszthetjük bármely függvényre, olyanokra is, amelyek nem a térbeli pozíciónak az időbeli függvényei.
Egy f függvény átlagos változását egy a-tól a + h-ig terjedő intervallumon úgy definiálhatjuk, mint 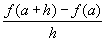 . Ezt az arányt nevezzük különbségi hányadosnak, mely nem más, mint a függvénykimenet változása osztva
a bemenet változásával. Hasonlóan általánosíthatjuk a pillanatnyi sebesség fogalmát is a függvény pillanatnyi változásának
fogalmaként, nevezetesen úgy, hogy a különbségi hányados határértékét képezzük, amint h közelít 0-hoz.
Precízebben megfogalmazva, az f függvény változását valamely a pontban az f a pontbeli deriváltjának nevezzük,
f ' (a)-val jelöljük, és így definiáljuk:
. Ezt az arányt nevezzük különbségi hányadosnak, mely nem más, mint a függvénykimenet változása osztva
a bemenet változásával. Hasonlóan általánosíthatjuk a pillanatnyi sebesség fogalmát is a függvény pillanatnyi változásának
fogalmaként, nevezetesen úgy, hogy a különbségi hányados határértékét képezzük, amint h közelít 0-hoz.
Precízebben megfogalmazva, az f függvény változását valamely a pontban az f a pontbeli deriváltjának nevezzük,
f ' (a)-val jelöljük, és így definiáljuk:
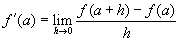 .
.
Ha a fenti határérték létezik, akkor azt mondjuk, hogy az f függvény differenciálható az a pontban.
Próbálja ki a következőket:
- Az applet kiindulásképpen egy parabolát mutat. Mi ennek a függvénynek a deriváltja az x = 1 pontban?
A zöld egyenes az (1; 1) és (1.9; 3.61) pontokon átmenő szelőt ábrázolja. E szelő meredeksége
megegyezik a függvény 1 és 1.9 közti intervallumára eső átlagos változásával.
Ha a zöld pöttyöt a piros felé húzza, azzal lényegében a h értékét csökkenti a különbségi hányadosban,
így a szelő meredeksége az 1 pontbeli deriválthoz fog közelíteni. A piros egyenes a görbe érintője az
x = 1 pontban, vagyis a piros egyenes meredeksége megegyezik az 1 pontban vett deriválttal.
- Kattintson rá a Zoom In gombra! Mi történik a parabolagörbe meredekségével?
Nagyítson bele a grafikonba még néhányszor! Milyennek látszik a fekete parabolagörbe a piros érintőhöz képest?
Ahogyan belenagyít a függvény egy pontjába, ahol létezik derivált, úgy válik a függvénygörbe egyre hasonlóbbá
egy egyeneshez, egészen pontosan az érintőhöz.
- Válassza ki a második példát a legördülő menüből! Ez a példa egy szinuszgörbét mutat radiános beosztású vízszintes tengellyel.
Mi a függvény deriváltja az x = π pontban? Húzza el a zöld pöttyöt és figyelje meg, miként
változik a szelő meredeksége, s miként közelít az érintő meredekségéhez! Így a sin(x) deriváltja a π pontban -1.
- Kattintson rá néhányszor a Zoom In gombra! Figyelje meg, hogy a szinuszgörbe egyre hasonlóbbá válik az érintő egyeneshez!
- Válassza ki a harmadik példát a legördülő menüből! Ez egy exponenciális függvény. Mi a deriváltja az x = 0 pontban?
A zöld pötty elhúzásával, vagy a piros érintő meredekségének megfigyelésével megkapja a választ. Nagyítással a görbe fokozatosan belesimul az érintőbe.
- Válassza ki a negyedik példát, egy hiperbolát! Mi a derivált az x = 1 pontban? A zöld pötty elhúzásával, vagy a piros érintő meredekségének megfigyelésével megkapja a választ.
Nagyítással a görbe fokozatosan belesimul az érintőbe.
- Ön is beírhat tetszőleges függvényképleteket a "f(x)=" mezőbe.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
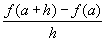 . Ezt az arányt nevezzük különbségi hányadosnak, mely nem más, mint a függvénykimenet változása osztva
a bemenet változásával. Hasonlóan általánosíthatjuk a pillanatnyi sebesség fogalmát is a függvény pillanatnyi változásának
fogalmaként, nevezetesen úgy, hogy a különbségi hányados határértékét képezzük, amint h közelít 0-hoz.
Precízebben megfogalmazva, az f függvény változását valamely a pontban az f a pontbeli deriváltjának nevezzük,
f ' (a)-val jelöljük, és így definiáljuk:
. Ezt az arányt nevezzük különbségi hányadosnak, mely nem más, mint a függvénykimenet változása osztva
a bemenet változásával. Hasonlóan általánosíthatjuk a pillanatnyi sebesség fogalmát is a függvény pillanatnyi változásának
fogalmaként, nevezetesen úgy, hogy a különbségi hányados határértékét képezzük, amint h közelít 0-hoz.
Precízebben megfogalmazva, az f függvény változását valamely a pontban az f a pontbeli deriváltjának nevezzük,
f ' (a)-val jelöljük, és így definiáljuk: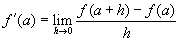 .
.