Differenciálhatóság
Az f függvényt differenciálhatónak mondjuk az a helyen, ha a különbségi hányadosnak létezik határértéke (vagyis ha 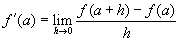 létezik). A jelen appletben azt vizsgáljuk meg, hogy mit is jelent ez közelebbről.
létezik). A jelen appletben azt vizsgáljuk meg, hogy mit is jelent ez közelebbről.
Próbálja ki a következőket:
- Az applet először egy szakadásos egyenest mutat.
Mi a függvény deriváltja az x = 1 pontban? Húzza el lassan a zöld pöttyöt a piros pötty felé!
Hogyan változik a zöld szelő meredeksége? Miért?
Most húzza a zöld pöttyöt a piros pötty baloldalára, majd lassan közelítsen vele a piros pötty felé!
Most hogyan változik a szelő meredeksége?
Amikor a zöld pöttyöt jobbról húzzuk a piros pötty felé, akkor voltaképpen egy nullánál nagyobb h értékből indulunk ki
és azt egyre kisebbre vesszük. Ha létezik ekkor határérték, azt jobboldali deriváltnak nevezzük és így
definiáljuk:
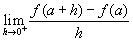 .
A nulla melletti + jel mutatja, hogy jobboldali határértékről van szó.
Hasonlóan, amikor a zöld pöttyöt balról húzzuk a piros pötty felé, akkor voltaképpen egy nullánál kisebb h értékből indulunk ki
és azt egyre közelítjük nullához. Ha létezik ekkor határérték, azt baloldali derviáltnak nevezzük, és így
definiáljuk:
.
A nulla melletti + jel mutatja, hogy jobboldali határértékről van szó.
Hasonlóan, amikor a zöld pöttyöt balról húzzuk a piros pötty felé, akkor voltaképpen egy nullánál kisebb h értékből indulunk ki
és azt egyre közelítjük nullához. Ha létezik ekkor határérték, azt baloldali derviáltnak nevezzük, és így
definiáljuk: 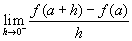 .
Ebben a példában a függvényünknek létezik jobboldali deriváltja az x = 1 pontban és egyenlő 1-gyel
(ennyi a jobboldali egyenes meredeksége). Ugyanakkor a baloldali derivált meghatározatlan, mivel végtelenhez tart, ha
h nullához közelít.
Így ez a függvény nem differenciálható az x = 1 helyen. Az elmondottak minden szakadásos függvényre érvényesek.
.
Ebben a példában a függvényünknek létezik jobboldali deriváltja az x = 1 pontban és egyenlő 1-gyel
(ennyi a jobboldali egyenes meredeksége). Ugyanakkor a baloldali derivált meghatározatlan, mivel végtelenhez tart, ha
h nullához közelít.
Így ez a függvény nem differenciálható az x = 1 helyen. Az elmondottak minden szakadásos függvényre érvényesek.
- Válassza ki a második példát a legördülő menüből! Ez egy egyenes, melynek az egyik pontját áthelyeztük
(oda, ahol a piros pötty van). Mennyi a függvény deriváltja az x = 1 pontban?
Húzza lassan el a zöld pöttyöt a piros pötty felé! Hogyan változik a zöld szelő meredeksége?
Most húzza a zöld pöttyöt a piros pötty baloldalára, majd lassan közelítsen vele a piros pötty felé!
Hogyan változik a meredekség? Most sem baloldali, sem jobboldali derivált nem létezik
(mindkettő végtelenbe tart), így a függvény nem differenciálható az x = 1 helyen.
- Válassza ki a harmadik példát! Ez egy olyan egyenes, amelynek hézagpontja van.
Mennyi a függvény deriváltja az x = 1 pontban? Ebben az esetben a függvény nincsen értelmezve az x = 1 pontban,
így bizonyos értelemben nem "fair" a kérdés, hogy a függvény vajon differenciálható-e itt vagy sem.
Egy függvényt nem tekintünk differenciálhatónak olyan bemenő értékeken, amelyek kívül esnek a függvény értelmezési tartományán.
- Válassza ki a negyedik példát, mely egy függőleges aszimptotájú hiperbolát mutat!
Mennyi a függvény deriváltja az x = 1 pontban? Az előző példához hasonlóan a függvény nincs definiálva az x = 1 pontban,
ezért nem differenciálható itt. Ezek a példák azt illusztrálják, hogy egy függvény nem differenciálható olyan helyen, ahol nem vesz fel értéket, vagy nem folytonos.
- Válassza ki az ötödik példát, mely az abszolútérték függvényt mutatja
(az áttekinthetőség miatt eltoltuk jobbra fölfelé)! Mennyi a függvény deriváltja az x = 1 pontban?
Most van függvényérték az x = 1 pontban és a függvény folytonos itt.
Húzza el a zöld pöttyöt jobbról a piros pötty felé, majd tegye ugyanezt balról is! Hogyan változik a zöld szelő meredeksége a két esetben?
Példánkban mind a baloldali, mind a jobboldali határérték létezik, ám különbözőek.
Ilyen esetben nem létezik általános derivált (emlékezzen vissza, hogy általános határérték csak akkor létezett, ha a kétoldali határértékek léteztek és megegyeztek),
ezért a függvény nem differenciálható az x = 1 pontban.
A szegletek, amilyen ez is, ott jönnek létre, ahol a meredekség ugrásszerűen megváltozik, melynek köszönhetően a jobboldali és baloldali határértékek különbözőek lesznek.
- Válassza ki a hatodik példát! Ez egy hatványfüggvény, melynek a grafikonja olyan, hogy a két íve éles csúcsban találkozik.
A függvény folytonos az x = 0 pontban. Létezik derivált az x = 0 pontban?
Húzza el a zöld pöttyöt a piros pötty felé először jobbról, majd balról, és figyelje a meredekséget!
Ahogy a szegletek, úgy az éles csúcsok is ugrásszerűen megváltoztathatják a meredekséget, így a függvény nem differenciálható
az x = 0 pontban.
- Válassza ki a hetedik példát, egy köbgyök függvényt! Ez is folytonos az x = 0 pontban,
de vajon differenciálható itt? Húzza el a zöld pöttyöt a piros pötty felé! A piros pötty közelében a meredekség láthatóan igen nagyra nő.
Még közelebb férkőzhet a piros pöttyhöz, ha az x mezőbe írja be az értékeket, mondjuk 0.00001-et.
A helyzet az, hogy a köbgyök függvénynek függőleges érintője van az x = 0 pontban,
ami azt jelenti, hogy a deriváltban szereplő határérték meghatározatlan ebben a pontban.
Így ez a függvény nem differenciálható az x = 0 pontban.
Általánosságban elmondható, hogy egy függvény nem differenciálható olyan helyen, ahol függőleges érintője van.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
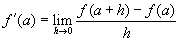 létezik). A jelen appletben azt vizsgáljuk meg, hogy mit is jelent ez közelebbről.
létezik). A jelen appletben azt vizsgáljuk meg, hogy mit is jelent ez közelebbről.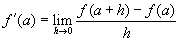 létezik). A jelen appletben azt vizsgáljuk meg, hogy mit is jelent ez közelebbről.
létezik). A jelen appletben azt vizsgáljuk meg, hogy mit is jelent ez közelebbről.