A második derivált becslése táblázattal
Korábban megmutattuk, hogyan lehet táblázat segítségével megközelíteni a derivált függvényt.
Most nézzük meg, hogyan tudunk a második deriváltról becslést adni a táblázatban feltüntetett értékekből!
Próbálja ki a következőket:
- Az applet egy olyan táblázatot mutat, mely kiragadott függvényértékeket tartalmaz.
Az első sor kiválasztott x értékeket tartalmaz, a második sor feltünteti a megfelelő
f (x) értékeket. A harmadik sorban a derivált becsült értékeit találjuk, a negyedik sor pedig a második deriváltra ad becsléseket.
A második derivált becsléseit az első derivált becsléseiből alkotott párokból és azokból az x pontpárokból számoljuk ki,
melyek az első deriváltra adott becsléseknél használt x intervallumokat a táblázatban közrefogják.
Például a táblázatban feltüntetett második deriváltra adott első becslést a következőképpen számoltuk ki:
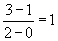 , ahol a 3 és az 1 a táblázatban közvetlenül a második derivált fölött
található két, az első deriváltra adott becslés, míg a nevezőben álló 2 és 0 az első deriváltra adott becslés kiszámításánál használt
x szélsőértékek. Megjegyzendő, hogy mivel az első derivált adbecslései egy x intervallumot fogtak át, így a
második derivált becslése két x intervallumot fog át. Ki tud számolni további becsléseket a második deriváltra a táblázat adataiból?
, ahol a 3 és az 1 a táblázatban közvetlenül a második derivált fölött
található két, az első deriváltra adott becslés, míg a nevezőben álló 2 és 0 az első deriváltra adott becslés kiszámításánál használt
x szélsőértékek. Megjegyzendő, hogy mivel az első derivált adbecslései egy x intervallumot fogtak át, így a
második derivált becslése két x intervallumot fog át. Ki tud számolni további becsléseket a második deriváltra a táblázat adataiból?
- Válassza ki a második példát a legördülő menüből! Ez ugyanaz a függvény, csak most az x pontok
távolabb esnek egymástól.
- Válassza ki a harmadik példát, egy lineáris függvényt! Számoljon ki egy-két becslést a második deriváltra
és ellenőrizze, hogy megegyeznek-e a táblázatban feltüntetett értékekkel! Mit vesz észre a második deriválttal kapcsolatban?
- Válassza ki a negyedik példát, egy konstans függvényt! Vajon miért azonosan 0 a második derivált értéke?
- Válassza ki az ötödik példát, egy exponenciális függvényt! Lát-e valami összefüggést a derivált, a második derivált és
a függvényérték között? Később még visszatérünk erre.
- Válassza ki a hatodik példát, egy hiperbolát! Az első derivált becslései mind negatívak, a második derivált
becslései viszont mind pozitívak. Miért?
- Ön is összeállíthat példákat, tetszőleges függvényképletet beírva a
"f(x)= " mezőbe. Továbbá megválaszthatja az x kezdőértéket és
az x értékek közti lépéseket is.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
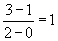 , ahol a 3 és az 1 a táblázatban közvetlenül a második derivált fölött
található két, az első deriváltra adott becslés, míg a nevezőben álló 2 és 0 az első deriváltra adott becslés kiszámításánál használt
x szélsőértékek. Megjegyzendő, hogy mivel az első derivált adbecslései egy x intervallumot fogtak át, így a
második derivált becslése két x intervallumot fog át. Ki tud számolni további becsléseket a második deriváltra a táblázat adataiból?
, ahol a 3 és az 1 a táblázatban közvetlenül a második derivált fölött
található két, az első deriváltra adott becslés, míg a nevezőben álló 2 és 0 az első deriváltra adott becslés kiszámításánál használt
x szélsőértékek. Megjegyzendő, hogy mivel az első derivált adbecslései egy x intervallumot fogtak át, így a
második derivált becslése két x intervallumot fog át. Ki tud számolni további becsléseket a második deriváltra a táblázat adataiból?