Kétszeres differenciálhatóság
Egy függvény lehet differenciálható egy pontban, de nem feltétlenül differenciálható ott kétszer
(ekkor az első derivált létezik, a második azonban nem).
Próbálja ki a következőket:
- Az első grafikon egy köbfüggvényt mutat, melyet jobbra felfelé eltoltunk, hogy a koordinátatengelyek ne legyenek útban.
Figyelje meg, hogy létezik deriváltja az x = 1 pontban, és hogy a derivált (középen) ugyancsak differenciálható az x = 1 pontban.
Tologassa a csúszkát, hogy megbizonyosodjon róla, nem történnek éles változások! Így erről a függvényről azt mondjuk, hogy kétszer differenciálható az x = 1 pontban.
- A második példa egy fél parabolát mutat, amely egy fél köbfüggvényhez csatlakozik. A grafikont most is eltoltuk jobbra felfelé.
A függvényt a következő képlettel adjuk meg:
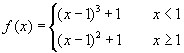 .
A középső ábra mutatja a deriváltat, amely létezik az x = 1 pontban, hiszen
a jobboldali és baloldali deriváltak megegyeznek ebben a pontban (mindkettő 0).
Ugyanakkor nézze meg a középső ábrán az első derivált grafikonját: differenciálható az x = 1 pontban
(azaz kétszer differenciálható az eredeti függvény)?
Mozgassa a csúszkát és vegye észre, hogy az első deriváltnak szeglete van az x = 1 pontban!
Ezért az első derivált nem differenciálható ezen a helyen.
.
A középső ábra mutatja a deriváltat, amely létezik az x = 1 pontban, hiszen
a jobboldali és baloldali deriváltak megegyeznek ebben a pontban (mindkettő 0).
Ugyanakkor nézze meg a középső ábrán az első derivált grafikonját: differenciálható az x = 1 pontban
(azaz kétszer differenciálható az eredeti függvény)?
Mozgassa a csúszkát és vegye észre, hogy az első deriváltnak szeglete van az x = 1 pontban!
Ezért az első derivált nem differenciálható ezen a helyen.
- Talán észrevette, hogy az előző példában az x = 1 pontban a második derivált grafikonja hézagpontot jelez az (1,2) pontban,
miközben az applet a grafikonon található kis kijelzőn azt mutatja, hogy f '' (1) = 2,
következésképpen hogy létezik második derivált. Melyik az igaz? Valójában a második derivált nem létezik,
mint azt feljebb megjegyeztük, ám a grafikai szoftver nem elég okos ahhoz, hogy felismerje ezt, így azt gondolja, hogy létezik második derivált.
Ezért tűnik fel a kis kijelzően az, hogy a második derivált értéke 2, miközben valójában annak kéne megjelennie, hogy "undefined", azaz "nincs értelmezve."
A hézagpontot nem ábrázolja a szoftver, mi rajzoltuk hozzá a példához, hogy a grafikon világosabb legyen.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
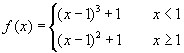 .
A középső ábra mutatja a deriváltat, amely létezik az x = 1 pontban, hiszen
a jobboldali és baloldali deriváltak megegyeznek ebben a pontban (mindkettő 0).
Ugyanakkor nézze meg a középső ábrán az első derivált grafikonját: differenciálható az x = 1 pontban
(azaz kétszer differenciálható az eredeti függvény)?
Mozgassa a csúszkát és vegye észre, hogy az első deriváltnak szeglete van az x = 1 pontban!
Ezért az első derivált nem differenciálható ezen a helyen.
.
A középső ábra mutatja a deriváltat, amely létezik az x = 1 pontban, hiszen
a jobboldali és baloldali deriváltak megegyeznek ebben a pontban (mindkettő 0).
Ugyanakkor nézze meg a középső ábrán az első derivált grafikonját: differenciálható az x = 1 pontban
(azaz kétszer differenciálható az eredeti függvény)?
Mozgassa a csúszkát és vegye észre, hogy az első deriváltnak szeglete van az x = 1 pontban!
Ezért az első derivált nem differenciálható ezen a helyen. 