Kalkulus Appletek

Mozgásegyenlet

Tudjuk, hogy amennyiben ismerjük egy mozgó objektum hely-idő függvényét s (t), akkor meg tudjuk határozni a sebesség függvényét v(t), úgy, hogy deriváljuk az s-t, és meg tudjuk határozni a gyorsulás függvényét is, amennyiben deriváljuk v-t. Most tegyük fel, hogy a gyorsulás függvénye adott, valamint a kezdeti sebesség és a kezdeti hely. Használva az "antideriválás"-t megkapjuk v-t és s-t. Legyen a(t) a gyorsulás függvény, v₀ a kezdeti sebesség és s₀ a kezdeti hely. Oldjuk meg a következő differenciálegyenletet 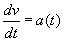, amely megoldásaként kapjuk v(t)-t (ahol C, az integrációs konstans most v₀ lesz). Most, hogy már ismerjük v-t, meg tudjuk oldani a következő differenciálegyenletet: 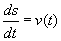, amely megoldásaként megkapjuk a hely-idő függvényt (ahol C, az integrációs konstans most s₀ lesz).

Próbálja ki a következőket!

1. Az applet 3 grafikont mutat: a(t) függvényt a bal oldali grafikon, v(t) függvényt a középső grafikon és s(t) függvényt a jobb oldali grafikon. Ebben a példában a gyorsulás -9.8 m/sec² (vagyis egy, a Föld felszínéhez közeli, szabadon eső testről van szó). A bal oldali grafikonon a vízszintes tengely "alatti" terület 0-tól egy t időpontig, piros. Mozgathatja a csúszkát az időpont változtatásához! Vegye észre, hogy a terület a bal oldali grafikonon ugyanakkora, mint a középső grafikonon a függvényérték! A sebesség az "antiderivált"-ja a gyorsulásnak. Ebben a példában, 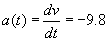, tehát 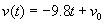. Ez egy egyenes lesz a középső grafikonon.
   
   
2. Most figyeljük a középső grafikonon a színezett területet, és vegyük észre, hogy ez ugyanaz az érték, mint a jobb oldali grafikonon a függvényérték! Ebben a példában 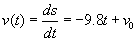, így megkaphatjuk 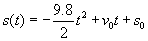, amely egy parabola a jobb oldali grafikonon. Emlékezzen , hogy a parabola nem a test mozgásának pályája! Jelen esetben egy egydimenziós mozgást vizsgálunk és a jobb oldali grafikon a test helyét mutatja az idő függvényében (azaz a felszíntől való magasságát).
   
   
3. Mozgassa v₀ csúszkáját és figyelje milyen következménye lesz a kezdeti sebesség (azaz v a t = 0-ban) változtatásának! Mozgassa az s₀ csúszkát és figyelje mi történik, ha a kezdeti hely (azaz s a t = 0-ban) változik!
   
   
4. Ki lehet próbálni más, összetettebb gyorsulás függvényeket is. Midhárom grafikon mozgatató, kicsinyíthető és nagyítható a szokásos módon.

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.