Exponenciális függvények
Az exponenciális függvények annyiban speciálisak, hogy a deriváltjaik nagyon hasonlítanak az eredeti függvényre, mint azt a korábbi példáknál láthattuk.
Próbálja ki a következőket:
- Az első példa egy olyan exponenciális függvényt mutat, melynek alapja k konstans szám (a példa kiindulóértéke 5). Hogyan néz ki a derivált?
Eléggé hasonló az eredeti exponenciális függvényhez, csak meredekebben emelkedik. Mozgassa a k csúszkát és figyelje meg, hogyan változik a derivált alakja.
Vannak olyan k értékek, melyekre a derivált kevésbé meredeken emelkedik, mint az eredeti görbe? Melyik k értéknél válik a két görbe egyformává?
Még közelebb juthat ehhez a bűvös k értékhez, ha az x = 1 beállításnál megnézi, milyen értéket ad f '(1) (a grafikon jobboldalán látható rubrikában),
amikor a k csúszkát mozgatja. Mivel f (1) = k, ha f ' (1) = k, így a két görbe azonos. Ha már közel jutott a keresett k értékhez a csúszka használatával,
finomhangolást is végezhet a k értéken a billentyűzet jobb és bal nyilaival. Azt fogja látni, hogy k ≈ 2.718 értéknél a függvény megegyezik a deriváltjával.
A precíz válasz: k = e. Csakugyan, gépeljen "e"-t a k mezőbe és a két görbe azonossá válik! Tehát
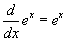 .
.
- Mi a helyzet az e-től különböző alapokkal? Úgy tűnik, hogy a derivált hasonló az eredeti exponenciális függvényhez, de elnyúltabb vagy meredekebb.
Csakugyan így van, és a deriválási formula így szól:
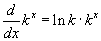 .
.
- Mi történik akkor, ha 0 < k < 1? Válassza ki a második példát a legördülő menüből! Ez ugyanaz a függvény, csak most a k csúszka
a 0 és 5 közötti értékeken mozgatható (míg az előző példában 1 és 5 között mozgott). Mi történik a derivált görbével? Miért?
Mit jelent egy 0 és 1 közé eső szám logaritmusa? A fentebb megadott szabály még most is érvényes.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
