Konstans, lineáris és hatványfüggvény deriváltja
Ebben a szakaszban a deriváltak kiszámításához használt formulákat mutatjuk be. E formulák kombinálásával meghatározhatod
azoknak a függvényeknek a deriváltjait, melyek képletében az alapfüggvények valamilyen kombinációja szerepel.
Először konstans, majd lineáris, végül hatványfüggvényeket fogunk megnézni
(hiszen a konstans függvények és az origón átmenő lineáris függvények speciális esetei a hatványfüggvényeknek).
Egy hatványfüggvényt a következő képlettel adhatunk meg: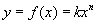 
ahol k és n valós számok.
Próbálja ki a következőket:
- Az első példa az f (x) = k konstans függvényt mutatja
(vagyis egy olyan hatványfüggvényt, ahol n = 0). Kiindulásnál k értéke 1.
A függvény egy vízszintes egyenes, amit elfed a piros érintő.
Mozgassa az x csúszkát és figyelje a célkereszt mozgását. Mi a derivált függvény? Mozgassa a k csúszkát: változik-e a derivált?
Konstans függvény deriváltja mindig 0, azaz
.
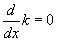- Válassza ki a második példát a legördülő menüből! Ez egy origón átmenő, k meredekségű egyenes.
A piros érintő, mint az előző példánál, itt is elfedi a függvényt. Mozgassa az x csúszkát: mi a derivált függvény, és mi a kapcsolata k-val?
Mozgassa a k csúszkát: hogyan változik a derivált? Az origón átmenő egyenes deriváltja egy konstans függvény, melynek értéke megegyezik az egyenes meredekségével, azaz
.
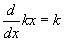Ennek van értelme, hiszen a derivált egy függvény grafikonjának a meredekségéről nyújt információt és az egyenes meredeksége mindenütt konstans.
- Válassza ki a harmadik példát, mely egy parabolát ábrázol! Mi a deriváltja? Mozgassa az x csúszkát és győződjön meg róla, hogy a derivált függvény
egy kiválasztott x pontban megadja a parabola meredekségét ebben a pontban (ebben a példában nem használjuk a k csúszkát).
Mi a derivátlt egyenlete (tipp: az x = 1 beállítással könnyebben megtalálja a deriváltfüggvény meredekségét)? Egy közönséges parabola deriváltja
egy 2 meredekségű egyenes, azaz
.
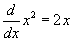- Válassza ki a negyedik példát, mely egy köbfüggvényt mutat! Mi a deriváltja? Mozgassa az x csúszkát és győződjön meg róla, hogy a derivált függvény
egy kiválasztott x pontban megadja a köbfüggvény meredekségét ebben a pontban (ebben a példában nem használjuk a k csúszkát).
Mi a derivátlt egyenlete (tipp: az x = 1 beállítással könnyebben megtalálja a deriváltfüggvény meredekségét)? Egy közönséges köbfüggvény deriváltja
egy közönséges parabola 3-szorosa, azaz
.
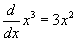- Válassza ki az ötödik példát, mely egy negyedfokú hatványfüggvényt mutat! Hogyan néz ki a deriváltja? Ez nem más, mint
.
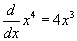Észrevett valami ismétlődő szabályszerűséget ezeknél a deriváltaknál? Vajon egy hatványfüggvény deriváltja szintén hatványfüggvény?
Mi történik a kitevővel a deriválásnál? Mi a konstans szorzó a derivált előtt? Talán kitalálta, hogy egy hatványfüggvény deriváltját
a következő egyszerűbb eljárással kaphatjuk meg: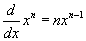 
.
Ez a hatványszabálynak nevezett formula azt mondja, hogy egy egyszerű hatványfüggvény deriváltját úgy kapjuk meg, hogy
a kitevőből kivonunk 1-et és szorzótényezőként elé írjuk az eredeti hatványkitevőt.
- Válassza ki a hatodik példát! Itt k a kitevő és az értéke -5 és 5 közötti egész szám. Vajon érvényes-e a hatványszabályunk mindezekre az értékekre?
Tologassa a k csúszkát, s főként vizsgálja meg a k = 0 és a negatív k eseteket. Valóban, a hatványszabály érvényes az egész kitevőkre, 0-t és a negatív egészeket is beleértve.
Megfigyelheti, hogy a páratlan negatív kitevőknél a grafikai szoftver hibásan megpróbálja összekötni a grafikon bal- és jobbfelét:
ez a hiba a szoftver korlátaiból ered.
- Válassza ki a hetedik példát! Ez ugyanaz, mint az előző, csak a k csúszka most nem egész értékeket vesz fel. Vajon még mindig érvényes a hatványszabály?
Kiinduló helyzetben k = 1/2, mely egy négyzetgyök függvényt eredményez. Mivel a szabályunk azt mondja, hogy ki kell vonni 1-et a kitevőből, így ezt kapjuk:
.
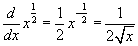Vagyis a hatványszabály négyzetgyök függvénynél is működik.
- Írjon be "1/3"-ot a k mezőbe, hogy köbgyök függvényt kapjon! A derivált furcsának tűnik, de továbbra is a hatványszabályt követi:
.
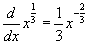Nézze meg, mi a derivált értéke x = 0-nál? A köbgyök függvénynek függőleges érintője van itt, ezért a derivált meghatározatlan.
Próbáljon meg más törteket beírni k rubrikájába! Figyelje meg, hogy amikor a nevező páratlan, a kapott grafikonnak pozitív és negatív oldala is van,
míg páros nevezőre csak pozitív oldala (persze a törtkitevő egyszerűsítése után: 2/6 nevezője páros, de a tört egyszerűsítve 1/3).
Figyelje meg azt is, hogy a grafikai szoftver néha hibásan összeköti a függvény vagy a deriváltja bal- és jobbfelét.
- Húzza a k csúszkát más valós kitevőértékekre! A szoftver megpróbálja átváltani ezeket egyszerűsített törtkitevőkre,
ha tudja, így néhány értéknél mindkét oldalt felrajzolhatja. A hatványszabály azonban továbbra is működik.
- Írjon be "pi"-t a k rubrikájába, és 1-et az x rubrikájába! Még mindig érvényes a hatványszabály?
Igen, érvényes minden valós számra, azaz:
.
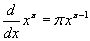- Mi az
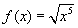függvény deriváltja?
Ez a példa egyszerűen megoldható, ha a négyzetgyököt (és más gyököket) kitevőkkel írja fel: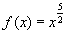 
.
Ezután már csak alkalmazni kell a hatványszabályt, hogy megkapja a deriváltat.
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.