A határérték formális meghatározása
Eddig "közelítések" segítségével beszéltünk a határértékekről és azt taglaltuk, hogy hogyan gondoljuk el szemléletesen őket. A határérték fogalmát a következőképpen tehetjük precízebbé és formálisabbá:
- Először is definiáljunk néhány kifejezést! L legyen továbbra is a határérték, c legyen az a bemenő érték, amelyhez tartozó határértéket meg akarjuk találni, végül f (x) legyen a függvény.
- A következő lépésben tegyük formalizáltabbá azt, hogy mit értünk c-hez közelítésen!
Az egyik útja ennek az, hogy veszünk egy c körüli intervallumot, amely pozitív és
negatív irányokba is kiterjed egy bizonyos δ (delta) mennyiséggel. Az intervallumot írhatjuk így: c - δ < x < c + δ, vagy rövidebben: |x - c| < δ (azaz x benne van c δ sugarú környezetében).
Mivel a határérték a c-hez közelítésen múlik és nem a c-beli értéken,
ezért hozzáfűzzük azt a feltételt, hogy x ≠ c. Továbbá kikötjük azt is, hogy δ nagyobb 0-nál.
Így ezen elgondolás szerint a c-hez közelítés azt jelenti, hogy összezsugorítjuk az intervallumot,
vagyis a δ-t egyre kicsinyítjük.
- Hasonlóan, vehetünk egy L körüli intervallumot is egy mindkét irányba kiterjedő
ε (epszilon) mennyiséggel: |f (x) - L| < ε
(azaz f (x) benne van L ε sugarú környezetében).
Az L-hez közelítést úgy gondoljuk el, hogy ε egyre zsugorodik (noha, mint fentebb, ε nagyobb 0-nál).
- Most valahogyan kapcsolatot kell teremtenünk a két intervallum között. Vegyünk egy meghatározott
ε értéket, mely megad egy intervallumot az L körüli függvényértékekhez!
Ha L a határérték, amikor x közelít c-hez, akkor tudnunk kell találni egy olyan
c körüli intervallumot, amelyre teljesül az, hogy minden ezen intervallumon belül felvett függvényérték
benne marad L ε sugarú környezetében. Lehet, hogy ehhez a δ értéket roppant kicsinnyé kell tennünk,
de ha találunk ilyen értéket, akkor L esélyes a határértékre, hiszen kizártuk azt, hogy a függvényértékek végtelenhez tartsanak, ha c-hez közelítünk,
és azt is, hogy a függvényértékek jobban oszcilláljanak vagy ugrándozzanak
az ε és az L által közrefogott távolságnál. Ugyanakkor ε-nál kisebb mértékben oszcillálhatnak vagy ugrándozhatnak a kimenő értékek.
- Végül válasszunk olyan ε-t, amilyent csak akarunk, akármilyen kicsit
(habár nagyobbat 0-nál)! Ha még mindig találunk hozzá olyan δ-t, amelyre
minden függvényérték L ε sugarú környezetén belül marad, akkor L-nek kell lennie a
határértéknek, hiszen nem hagytunk helyet oszcillálás vagy ugrándozás számára.
Mindezt belefoglalhatjuk a határérték formális definíciójába:
A 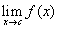 alatt azt az L számot értjük, amelyre teljesül, hogy minden
ε > 0 számhoz létezik olyan δ > 0 szám, hogy ha |x - c| < δ
és x ≠ c, akkor |f (x) - L| < ε.
alatt azt az L számot értjük, amelyre teljesül, hogy minden
ε > 0 számhoz létezik olyan δ > 0 szám, hogy ha |x - c| < δ
és x ≠ c, akkor |f (x) - L| < ε.
Próbálja ki a következőket:
- Az első grafikon egy korábbi példában szereplő egyenest mutat. Vajon a határérték L = 0.5, ha c = 1?
A függőleges halványzöld sáv ábrázolja a c δ sugarú környezetén belüli bemenő értékek intervallumát,
és a vízszintes rózsaszín sáv ábrázolja az L ε sugarú környezetén belüli függvényértékeket.
A formális definíciót alkalmazva megkérdezhetjük, hogy egy adott ε-hoz tudunk-e találni olyan δ-t,
hogy a függvény zöld sávon belüli része egyszersmind a rózsaszin sávba is beleessen.
A sárga keret a két sávnak a metszete, így tehát arra vagyunk kiváncsiak, hogy
a függvénygrafikonnak van-e olyan szakasza, amely a sárga keretből "átnyúlik" a zöld sávba.
A példát eredetileg úgy rajzoltuk fel, hogy az egyenesnek legyen olyan részlete, amely átnyúlik a zöld tartományba. Ez azt jelenti, hogy
a választott δ nem elég kicsi. Az applet alján található delta csúszka segítségével zsugorítsa össze a zöld sávot, amíg
a grafikonnak már nem lesz a sárga kereten kívüli része a zöld sávban (és ezzel a rózsaszin sávval is minden rendben lesz)! Ez azt jelenti, hogy a formális
definícióban foglalt feltételt kielégítettük egy adott ε értékre.
Az L-t akkor tekinthetjük határértéknek, ha képesek vagyunk bármely tetszőlegesen választott ε értékhez
a feltételnek megfelelő δ értéket találni. Az epszilon csúszkával kicsinyítse le ε-t úgy, hogy a grafikon
egy része megint átnyúljon a zöld sávba! Tud-e találni a delta csúszka mozgatásával olyan δ-t, amelyre
a grafikonnak már lesz a sárga kereten kívüli része a zöld sávban? Látni fogja, mindegy, hogy milyen kicsinyre választja az ε-t,
mindig talál hozzá a feltételnek megfelelő δ értéket. Ha igazán kicsi ε-t akar találni, akár egy pontba is zoomolhat a sárga keret közepén
a sárga négyzet közepére kattintva (mely kéteszeres zoomolást eredményez). Így a határérték L = 0.5, ha c = 1.
- Válassza ki a második példát! Ez ugyanaz mint az első, csak a függvény egy pontja át lett helyezve.
Vajon a határérték továbbra is L = 0.5, ha c = 1? Ha ugyanazt végigjátsza, mint az előbb,
látni fogja, hogy bármely kiválasztott ε értéknél összezsugoríthatja a δ-t úgy, hogy
a grafikonnak ne legyen a sárga kereten kívüli része a zöld sávban, kivéve az áthelyezett pont esetében. Ám ez a pont
nem jelent problémát, mivel a határérték meghatározásánál nem törődünk az f (c) értékkel.
Emlékezzen vissza, hogy a formális definíció alapján δ > 0 és x ≠ c, így ez a pont nem számít!
Ezért a határérték L = 0.5, ha c = 1.
- Válassza ki a harmadik példát! Ez hasonló az előző két esethez, csak most a függvénynek hézagpontja van.
Vajon a határérték továbbra is L = 0.5, ha c = 1? A dolgok ugyanúgy festenek, mint az előző példában,
csak most egy pont hiányzik. Bármely kiválasztott ε értéknél összezsugoríthatja a δ-t úgy, hogy
a grafikonnak ne legyen a sárga kereten kívüli része a zöld sávban. Ezért a határérték L = 0.5, ha c = 1.
- Válassza ki a negyedik példát! Vajon a határérték L = 1, ha c = 0?
Zsugorítsa a δ-t addig, amíg a grafikonnak már nem lesz a sárga kereten kívüli része a zöld sávban! Zoomoljon és
zsugorítsa az ε-t, majd keressen egy új megfelelő δ-t! Mindig sikerül? Minden ε-hoz
mindig tud δ-t találni? Igen, ezért a határérték L = 1, ha c = 0.
- Válassza ki az ötödik példát, egy szakadásos függvényt! Vajon a határérték L =
1.5, ha c = 1? Az eredeti ábrán lekicsinyítheti annyira δ-t, hogy a függvénygrafikonnak már ne legyen a sárga kereten kívüli része a zöld tartományban.
Azonban ha az ε-t kisebbre zsugorítja 0.5-nél, problémába ütközik: nincs olyan δ, amely elég kicsiny lenne ahhoz, hogy
a grafikon a sárga kereten belül maradjon. Ezért a határérték nem 1.5.
Lehet-e más érték? Próbálja meg L-t 2-re állítani az L csúszkával vagy értékmezővel! Amint látja,
ez sem működik. Ha az L lehetséges értékeit végignézi, látni fogja, hogy egyetlen érték sem működik.
Bármilyen értéket választ is, mindig létezik olyan ε, amelyre a grafikon átnyúlik a zöldbe, akármilyen
δ-t jelöl is ki. Ezért nincs határérték a c = 1 helyen.
- Válassza ki a hatodik példát, ezt a függőleges aszimptotájú függvényt! Mennyi a határérték, ha c = 1?
Nyilvánvalóan nem lehet 1.5, hiszen bárhogy is zsugorítja a δ-t a grafikon mindig felbukkan a zöldben
(habár kis δ értéknél a zöldbe eső rész kívül kerülhet az ablakon, ekkor a jobboldali egérgombbal átpásztázhatja
a grafikont, hogy megnézze ezt). Az L változtatása sem segít: akármilyen nagynak választja is L-t,
a grafikon egy része mindig bele fog esni a zöldbe. Ezért nincs határérték a c = 1 helyen.
- Válassza ki a hetedik példát, a tekergődző sin(1/x) függvényt! Vajon a határérték L = 0, ha c = 0?
A kiinduló ábrán az igen nagy 1.5-es ε érték mellett bármely δ működik, mivel a grafikon mindig benne marad a rózsaszín tartományban.
Ám ha az ε-t kisebbre zsugorítja 1-nél, a grafikon hullámai átlépnek a zöld tartományba.
A grafikon korlátozott felbontása miatt esetleg úgy vélheti, hogy megfelelő méretűre tudja szűkíteni δ-t,
ám ha belezoomol az ábrába, látni fogja, hogy a grafikon valójában még mindig annyira oszcillál, hogy itt-ott belenyúlik a zöldbe.
Ezért 0 nem határéreték a c = 0 helyen. Van-e más jó érték? Ha végignézi az
L lehetséges értékeit, azt fogja találni, hogy egyik sem jó. Mindig akad olyan ε, amely már elég kicsiny ahhoz, hogy a hullámok
benyúljanak a zöldbe, bármilyen δ értéket is választ. Ezért nincs határérték a c = 0 helyen.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
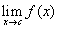 alatt azt az L számot értjük, amelyre teljesül, hogy minden
ε > 0 számhoz létezik olyan δ > 0 szám, hogy ha |x - c| < δ
és x ≠ c, akkor |f (x) - L| < ε.
alatt azt az L számot értjük, amelyre teljesül, hogy minden
ε > 0 számhoz létezik olyan δ > 0 szám, hogy ha |x - c| < δ
és x ≠ c, akkor |f (x) - L| < ε.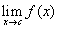 alatt azt az L számot értjük, amelyre teljesül, hogy minden
ε > 0 számhoz létezik olyan δ > 0 szám, hogy ha |x - c| < δ
és x ≠ c, akkor |f (x) - L| < ε.
alatt azt az L számot értjük, amelyre teljesül, hogy minden
ε > 0 számhoz létezik olyan δ > 0 szám, hogy ha |x - c| < δ
és x ≠ c, akkor |f (x) - L| < ε.