A kalkulus alaptétele
Az előző részekben láttuk, hogy a sebesség görbe alatti területe megadja a kezdeti ponttól megtett távolságot. Más szavakkal, ha s(t) az autó helyzete az adott t idopontban, és v(t) = s'(t) a sebessség, akkor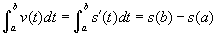 
, ahol s(b) - s(a) a tényleges távolság, ameddig a kezdeti a időponttól b időpontig eljutott. Kiderült tehát, hogy mi a kapcsolat egy függvény, a deriváltja és a határoztt integrálja között. Ez a kapcsolat, melyet a kalkulus alaptételének nevezünk, így hangzik: Ha f folytonos az [a,b] intervallumon, akkor 
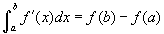. Más szavakkal, integrálva az f változásának mértékét egy intervallumra, az megadja az f függvény tényleges változását az adott intervallumon.
Próbálja ki a következőket!
- Az applet az f (x) függvényt ábrázolja a bal oldalon és a deriváltját f '(x)-et a jobb oldalon. Az f '(x) függvény alatti terület a és b között cián színűre festve a jobb oldalon látható, és az f (b) - f (a) különbséget a bal oldalon a cián színű oszlop mutatja az y tengelyen. Vegyük észre, hogy a különbség és a terület egyenlők, az adatok leolvashatók a grafikonok bal felső sarkában. Most mozgassuk a b csúszkát és rövidítsük az intervallumot. A terület természetesen csökken, és természetesen a különbség is. Hasonlóan változtatható az a értéke is, közelíthető b-hez. Tartsuk a értékét kevesebben, mint b értéke (ha véletlenül a értéke lesz a nagyobb b értékéhez képest, valami érdekes történik a terület értékével és a különbséggel; erre az estre egy későbbi részben visszatérünk). Ez a példa a konstans sebesség esetére vonatkozik.
- Nézzük a 2. példát a legördülő listáról! Ez egy harmadfokú függvényt és annak deriváltját mutatja. Az a és b csúszkát tudja mozgatni és megállapíthatja , hogy a terület és a különbség most is megegyezik (esetleg egy nagyon pici eltérés látható, de ez a kerekítési hiba következménye). Ez a példa megfelel a gyorsuló autó esetének.
- Nézzük a 3. példát a legördülő listáról! A normál parabolát és a deriváltját ábrázolja. Mozgassa az a csúszkát balra, és figyelje, hogy mi történik! Be tudja úgy állítani, hogy a terület és a különbség nulla legyen? Hol történik ez? Miért? (Vegye észre, hogy nem teljesen pontosan nulla, de lehetne nulla, a kerekítési hiba az oka a pontatlanságnak!)
- Itt is ki lehet próbálni saját függvényeket. Bizonyosodjon meg, hogy a függvény legalább az [a,b] intervallumon folytonos. Kicsinyíteni és nagyítani és mozgatni az ábrát a szokásos módon lehet.
This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.