A grafikus ábrázolással kapcsolatos problémák
A grafikai szoftvernek, mint amilyet ezek a weboldalak vagy a grafikai számológépek is használnak,
megvannak a maga korlátai. Ezen az oldalon bemutatunk ezek közül néhányat.
Próbálja ki a következőket:
- Vegyük az első példát, mely az y = x egyenest ábrázolja!
Az egyenes meredeksége miért nem 45°-os? A megoldás az, hogy az x és az y tengelyek más-más
skála szerint vannak beosztva. Így a körök is ellipszisnek látszanának. Kijavíthatjuk ezt az appleteken található
"Equalize Axes" gombra kattintva, mely a skálákat azonossá teszi.
- Válassza ki a második példát a legördülő menüből, ami egy másik egyenest mutat! Kattintson a "Equalize Axes" gombra, hogy
a skálák biztosan azonosak legyenek! Ha közelről megnézi az egyenest, észreveheti, hogy nem igazán sima, hanem olyan, mintha
lépcsőzetes lenne (apró lépcsőfokokból állna). Ezt a képernyő pixelei okozzák,
valamint az, hogy a grafikai szoftver nem számolja ki a grafikont minden egyes pixelre (csak minden harmadikra).
A 45° egyenesek elég simának tűnnek, de más szögek többé-kevésbé "recések" lehetnek.
- Válassza ki a harmadik példát! Ez egy
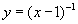egyenletű hiperbolát mutat.
Figyelje meg, hogy a grafikai szoftver a hiperbola jobb és a bal felét összekötötte, ami helytelen (egy függőleges aszimptotának kellene itt lennie). Ez a példa azt mutatja,
hogy a grafikai szoftver nem elég okos ahhoz, hogy felismerje, a részek összekötése helytelen. Ez a helyzet általában a grafikai számológépekkel is.
- Válassza ki a negyedik példát! Ez ugyanezt a hiperbolát mutatja, de immár az
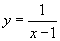egyenlet alapján.
Most a grafikai szoftver már ki tudja számolni, hogy a két részt nem szabad összekötni. Óvatosnak kell lennünk a függőleges aszimptotákat használó ábrázolásokkal, és mindig meg kell győződnünk róla,
hogy a grafikai szoftver által mutatott kép helyes-e vagy sem.
- Válassza ki az ötödik példát, mely az előbbi hiperbolát mutatja! Most fel van tüntetve egy függőleges aszimptota. Ezt valójában nem a grafikai szoftver hozza létre,
mely nem igazán tudja, hogy mi az a függőleges aszimptota. Hanem külön lett hozzárajzolva a példák szerkesztése során. Figyelje meg, hogy ha a kurzort
a függvény egyenletét mutató mezőre állítja és Enter-t nyom, a függőleges aszimptota eltűnik, mivel a szoftver azt hiszi, hogy egy új függvényt adott meg és ezért
törli a függőleges aszimptotát a példából.
- Válassza ki a hatodik példát, mely egy szakaszonként definiált függvényt mutat a végpontjaival együtt! Az utóbbi példához hasonlóan a grafikai szoftver nem elég okos ahhoz,
hogy kiszámolja, hol vannak a végpontok, és nyitottak-e vagy zártak. A feltüntetett végpontok külön lettek hozzárajzolva a pédához. Ha a kurzort a függvény
egyenletét mutató mezőre állítja és Enter-t nyom, a végpontok eltűnnek. Amikor a saját szakaszos függvényét írja be (vagy bármely olyan függvényt, amelynél
a végpontok fontosak), csak annyit fog látni, hogy a grafikon megszakad.
- Válassza ki a hetedik példát, mely egy hatványfüggvényt mutat! Vegye észre, hogy a példa egy köbgyök függvényt mutat, minden valós értékre mint értelmezési tartományra!
Bizonyos tankönyvek, melyek taglalják a komplex számokat is, csak a görbe pozitív felét ábrázolják, mintha négyzetgyök függvényről lenne szó. Mivel a jelen appleteket valós
függvényanalízishez szántuk, úgy döntöttünk, hogy mindkét oldalt ábrázoljuk, hogy az ábra összhangban legyen azzal, amit a diákok egy valós módban működő grafikai számológépen látnának.
Ha a függvény képletében szereplő tört nevezőjét 3-ról 2-re változtatja és Enter-t nyom, megjelenik a négyzetgyök függvény.
Próbáljon ki egyéb nevezőket is, párost és páratlant is. Aztán próbálja ki a "pi"-t. Ezt a grafikont várta? Vajon a pi páros vagy páratlan? A grafikai szoftver
most megpróbálja a kitevőt egy racionális törtre átváltani, a törtet egyszerűsíteni, és megnézni, hogy a számláló vagy a nevező páros-e vagy páratlan,
hogy meghatározza, szükséges-e ábrázolnia a grafikon negatív felét vagy sem. Mivel pi nem racionális szám, így a grafikai szoftver nem rajzolja fel a negatív részt.
Próbáljon 1001-et írni a nevező helyére: mi történik? 1001 páratlan szám, nem kéne akkor a negatív felet is felrajzolni? Ez mutatja a grafikai szoftver által használt
algoritmus korlátját, amellyel a kitevőt racionális számra próbálja átváltani: a szoftver feladja, ha a nevező nagyobb mint 1000. Próbálja ki a 999 nevezőt!
- Válassza ki a nyolcadik példát, mely egy szabályos szinuszgörbe! A számítógépétől függően a grafikon kinézhet szabályos szinuszgörbének, de az is lehet, hogy
egy kacskaringózó zagyvaságot fog látni. Ha szabályos szinuszgörbét lát, mi a periódusa? Megfelel a függvény képletében használt periódusnak? Próbálja mozgatni a csúszkát! A célkeresztnek
követnie kellene a grafikont, miért nem teszi? Próbáljon rákattintani a "zoom in" gombra,
vagy jelöljön ki egy periódust és nagyítsa fel azt! Mit lát? A probléma az, hogy a szinuszgörbe gyorsabban kigyózik a grafikai szoftver által használt
mintapontok számánál, ezért a grafikon csak mintapontokat mutat a görbéből és nem a valóságos görbét mutatja (mivel a periódusa ilyen rövid, az xmin-t nagyon közel kéne vinnie az xmax-hoz,
hogy lássa, milyen valójában a görbe). Ha az eredeti grafikonja egy lassan hullámzó szinuszgörbét mutatott, annak oka az, hogy a ténylegesen gyorsan kigyózó görbe mintapontjai
történetesen úgy rendeződtek sorba, hogy egy szabályos szinuszgörbére hasonlítanak. Ha belenagyít a grafikonba vagy megváltoztatja az xmin-t, a mintapontok máshová kerülnek
és a grafikon teljesen másként fog festeni. Kipróbálhatja azt is, hogy rákattint a "Restore limits" gombra, hogy visszatérjen a nagyítás előtti állapothoz, majd a függvény
képletében szereplő számot kisebbre változtatja, Enter-t nyom, és megnézi, hogyan néz ki most a grafikon. Mennyivel kisebbre kell változtatni a számot ahhoz, hogy szabályos szinuszgörbét kapjon?
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.