Növekedés, csökkenés és a logisztikus differenciálegyenlet
Az előző appletben láttuk, hogy a dy/dx = y differenciálegyenlet megoldása exponenciális függvény. Ebben a részben egy kicsit jobban megvizsgáljuk az ilyen típusú egyenletet.
Próbálja ki a következőket!
- Az applet a dy/dx = ky egyenlethez tartozó meredekségmezőt ábrázolja. Mozgassa k csúszkáját és figyelje mi történik a meredekségmezővel és a megoldásgörbével! Mi történik, amikor k nagy? És ha közel 0? Ha negatív? A változók szétválasztásának módszerével megkapjuk a megoldást
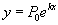. Mikor k pozitív, akkor egy növekvő függvényt kapunk, és amikor k negatív csökkenő a függvény. Ez a differrenciálegyenlet kiválóan alkalmas több különböző típusú probléma modellezésére, mint például egy populáció növekedése, a kamat halmozódása, és a radioaktív bomlás. Az ilyen típusú propblémákban a független változó általában t (ezzel jelöljük az időt) az x helyett. Szavakkal megfogalmazva az egyenlet szerint " y változásának mértéke, mely x-től függ, arányos y-nal," k konstans az arányossági tényező. Ha k pozitív, a változás mértéke egyre nagyobb lesz, egyre nagyobb y mellet. Megjegyezzük, hogy P0 az x = 0-hoz tartozó populáció, általában kezdeti populációnak nevezzük.
- Nézzük a 2. példát a legördülő listáról, ebben a példában a dy/dx = ky(1-y/L) egyenlet megoldását ábrázoljuk! Mozgassa k csúszkáját és figyelje a megoldás görbét! Ugyancsak mozgassa L csúszkáját (de legyen L > 1) és vegye észre mi történik! Az exponenciális növekedési modellekkel kapcsolatos egyik probléma az, hogy a valós populációk nem növekednek végtelenül. Az ebben a
példában szereplő egyenlet -amit logisztikus egyenletnek nevezünk- tartalmaz egy növekedési korlátot. A k még mindig meghatározza milyen gyors a növekedés, de L egy felső limitet biztosít a populációban. A megoldást a változók szétválasztásával kapjuk:
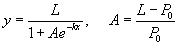ahol P0 a kezdeti populáció.
This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.