Kalkulus Appletek

Változók szétválasztása

Számos differenciálegyenlet nem oldható meg más módon, csak numerikus módszerekkel, vagy próbafüggvények kitalálásával és annak ellenőrzésével. Néhány azonban megoldható a csak x-től függő és a csak y-tól függő részek szétválasztásával, majd mindkét oldal integrálásával.

Próbálja ki a következőket!

1. Ez az applet a dy/dx = y egyenethez tartozó meredekségmezőt mutatja. A megoldás láthatóan exponenciális függvény. Tény, hogyha feltesszük, hogy y = e^x a megoldás, majd visszahelyettesítjük az egyenletbe, akkor tényleg meggyőződhetünk arról, hogy ez egy jó megoldás (azaz 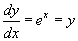). Módszeresebben tudunk eljárni, ha a megoldás kereséséhez a változók szétválasztása technikát választjuk. Vegyük a differenciálegyenletet és algebrai átalakítással végezzük el a következőt: vigyük az y-os tagokat a bal oldalra és az x-es tagokat a jobb oldalra! Kezeljük úgy a dy és dx tagokat, mintha független objektumok lennének és algebrai úton a megfelelő oldalra tegyük ezeket is! Ezek után integráljuk mindkét oldalt és egyszerűsítsünk! Erre a példára ez a következőképpen néz ki: 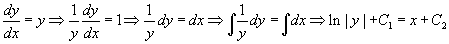. Az első lépésben elosztottuk mindkét oldalt y-nal, majd szoroztuk mindkét oldalt dx-szel. Integráltunk mindkét oldalon a megfelelő változó szerint és megkaptuk a megoldást. Vegye észre, hogy mindkét oldalon a megjelenő C-k tetszőleges konstansok, ezért ki tudjuk vonni egyiket mindkét oldalból és így összevonjuk őket egy új tetszőleges konstansba, tehát 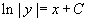! Vegyük az exponenciálisát az egyenletnek: 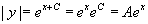, ahol e^C egy tetszoleges pozitív konstans, amit A>0-val jelölünk. Az abszolútérték jeltől megszabadulhatunk, ha megengedjük, hogy A negatív is lehet! Lehet A étéke 0? Ezt az esetet ellenőriznünk kell, mert amikor kezdetben osztottunk y-al mindkét oldalon, esetleg elveszítettük az y = 0 megoldást! Tény, hogy ez egy megoldás, tehát úgy tekinthetjük, hogy 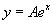adja a differenciálegyenlet megoldáshalmazát, ahol A tetszőleges valós szám.
   
   Változók szétválasztása csak akkor működik, ha y-t szorzással vagy osztással tudjuk a bal oldalra juttatni, nem kivonással vagy összeadással. Tehát például dy/dx = x + y nem szeparálható, de dy/dx = y + xy szeparálható, mert y kiemelhető a jobb oldali összegből és így mindkét oldal osztható y-nal. A dy/dx = (x + 3)/(y - 2) egyenlethez hasonló egyenletek ugyancsak szeparálhatóak, mivel mindkét oldalt meg tudjuk szorozni (y - 2)-vel; azzal nics gond, hogy konstans értéket mozgassunk. A kalkulus tankönyvekben további példákat talál szeparálható differenciálegyenletekre, amelyeket begépelve az appletbe meg tudja nézni a grafikonjukat (emlékezzen, hogyha a megoldás nem x függvénye, akkor a grafikus algoritmus elrontja az ábrázolást).

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.