Sorozatok
Egy számsorozat számok sorba rendezett halmaza. Például nézzük a követekező sorozatot 2, 4, 6, 8, ... a 2 a sorozat első eleme, 4 a második eleme, stb. Az sorozat n-edik tagjának jelölésére általában sn-t használunk. A sorozat tagjai lehetnek tetszőlegesek, lehetnek összefüggéssel megadva, mint például: sn = 2n. Általában egy sorozatban az n 1-gyel kezdődik, de előfordulhat, hogy a megfelelő választás n első elemének a 0, ebben az esetben az első tag s0. Amennyiben összeadjuk az első n elemét a sorozatnak, akkor részösszeget kapunk, általában így jelöljük: Sn (vagyis nagybetűvel).
Próbálja ki a következőket!
- Az applet egy sorotatot ábrázol, melyet a következő képlettel adunk meg: sn = 2 + 3(n - 1). Ez egy számani sorozat, mivel úgy kapjuk a tagjait sorban az előzőből, hogy mindig ugyanazt a számot adjuk hozzá (vagyis ebben a példában mindig 3-at adunk hozzá egy elemhez és így kapjuk a következőt). A számtani sorozat általános formulája: sn = s1 + d(n - 1), ahol s1 az első elem, d a differencia, vagy külnbség bármelyik szomszédos elem között (vagyis az a szám, amit mindig hozzá kell adni egy elemhez, hogy megkapjuk a következőt). Az első 10 tag részösszege az garfikon bal felső sarkában látható, és tudja változtatni a tagok számát, ha mozgatja a max n csúszkát, vagy beírja a max n mezőbe.
Az egyik terület, amely még érint minket amikor használjuk a sorozatokat, hogy mi történik a tagok értékeivel, amikor n végtelenhez tart. Másként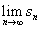 
-nek van értéke vagy sn végtelenhez vezet, vagy ugrál amikor n egyre nagyobb? Ha ez a határérték létezik, azt mondjuk, hogy a sorozat konvergál vagy konvergens. Ha a határérték nem létezik, a sorozat divergál vagy divergens. Nyilvánvaló, hogy a számtani sorozat divergens, mert a tagjai egyre nagyobbak lesznek.
- Nézzük a 2. példát a legördülő listáról, itt egy mértani sorozatot látunk, melyet így adunk meg: sn = 2n! A mértani sorozat minden elemét úgy kapjuk meg, hogy az előző tagot mindig ugyanazzal a számmál szorozzuk (a szorzó ebben a példában 2). A mértani sorozat általános formulája: sn = s1rn - 1, ahol r a hányados értéke (vagyis az a szám amellyel megszorozva egy tagot megkapjuk a következőt). Nyilánvaló, hogy r = 1 és r = 0 nem hasznos választások (mindkét esetben konstans sorozatot kapunk). A grafikon alapján érthető, hogy a példában megadott sorozat divergens, mivel a tagok egyre nagyobbak.
- Nézzük a 3. példát, amely egy másik mértani sorozatot ábrázol a hányados: 1/2! Ez a sorozat konvergens lesz? A tagok egyre közelebb lesznek zérushoz, tehát ez a sorozat konvergálni fog. A mértani sorozat konvergál, ha a hányados értéke 0 és 1 közöt van, és divergens, ha a hányados nagyobb mint 1.
- Nézzük a 4. példát, amely egy újabb mértani sorozatot mutat, amelynél negatív a hányados! Vegye észre, hogy a tagok alternálnak, azaz váltakozva találhatók a tengely pozitív és negatív oldalán! Ez a sorozat 0-hoz konvergál, így kiterjeszthetjük tudásunkat a mértani sorozatok konvergenciájáról, ha |r| < 1, akkor a sorozat konvergens.
- Ki tudja próbálni saját sorozatait, gépelje be a képletet, használja n-et mint változót!
This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.