Kalkulus appletek

Hiperbolikus függvények deriváltjai

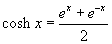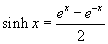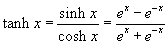Három hiperbolikus függvényt definiálunk, a következőképpen: , és . Az applet ezt a három függvényt és a deriváltjaikat mutatja be.

Próbálja ki a következőket:

1. Az első applet a cosh(x) grafikonját mutatja a baloldalon, a deriváltját a jobboldalon. A koszinusz hiperbolikusz egy parabolára hasonlít, ám a deriváltjára pillantva (mely a parabolánál egy egyenes) megállapíthatjuk, hogy a görbülete nem olyan, mint a paraboláé.
   
   
2. Válassza ki a második példát, mely a sinh(x) függvényt és a deriváltját mutatja! Nem tűnik ismerősnek? Menjen vissza az előző példához, majd nézze meg ismét a második példa grafikonját! Mit vesz észre? Csakugyan, 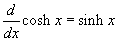és 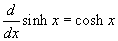. Jegyezze meg, hogy az egyszerű szinusztól és koszinusztól eltérően itt nem kell kitenni a minusz előjelet a cosh deriváltja elé.
   
   
3. Válassza ki a harmadik példát, mely a tanh(x) függvényt és a deriváltját mutatja! Bizonyára ki tudja számítani a deriváltat a tanh(x) képletéből a hányados deriválási szabályával. A derivált: .

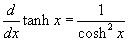Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.