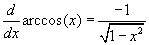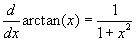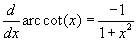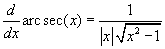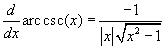Függvények inverzének deriváltja
Ha y = f (x), akkor az inverz viszonyt így fejezzük ki: y = f -1 (x). Ha az inverz szintén egy függvény, akkor azt mondjuk, hogy az f függvény invertálható.
Ebben az appletben az invertálható függvények deriváltjainak járunk utána.
Próbálja ki a következőket:
- Az applet az y = f (x) = 2x egyenest és az inverzét, az y = f -1 (x) = 0.5x függvényt mutatja.
A jobboldali grafikonon e két függvény deriváltjai láthatóak, mindkettő konstans függvény.
Az x csúszka tologatásával mozgathatja az x-hez tartozó f (x) függvénypontot (a lila grafikonon).
A lila pont koordinátái (x, f (x)). Az inverz függvényen is van egy pont, de ez a "tükörképe" az előbbi pontnak (azaz a koordinátái a lila pont koordinátáinak a felcserélt értékei).
A kék pont koordinátái tehát (f (x), x). E két ponthoz tartozó deriváltértékeket
a derivált grafikonjának jobb felső sarkában tüntettük fel, illetve célkereszttel is jelezzük magukon a grafikonokon.
Mivel a függvények lineárisak, így a deriváltak vízszintes egyenesek, az értékük konstans. Milyen kapcsolat van a két derivált között?
- Válassza ki a második példát a legördülő menüből, mely az y = f (x) = 3x egyenest és az inverzét, az y = f -1 (x) = (1/3)*x függvényt mutatja!
Milyen kapcsolat van a deriváltjaik között? Bizonyára észreveszi, hogy bármely pontot választ is ki, a deriváltak egymás reciprokai.
- Válassza ki a harmadik példát, mely egy fél parabolát és az inverzét, a négyzetgyökfüggvényt mutatja!
Még mindig fennáll a reciprok viszony a deriváltjaik között? Tologassa az x csúszkát és ellenőrizze, hogy így van-e
(ötlet: egész értékű deriváltak esetén könnyebb fejben kiszámolni a reciprokokat).
Ez a példa mutatja a két ponthoz tartozó érintőket is. Fontos észrevétel, hogy az inverz deriváltértékét nem azon a helyen számítjuk ki, ahol a függvény deriváltját, amint azt a
deriváltak grafikonjain látható célkeresztek is mutatják. Ha a függvény deriváltját az x = a helyen számítjuk ki, az inverz deriváltját az x = f (a) helyen számítjuk ki.
Ezzel megkapjuk az invertálható függvények általános deriválási formuláját:
.
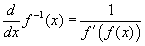A formula szerint egy függvény inverzének a deriváltja megegyezik a függvény deriváltjának az f (x) helyen vett reciprokával.
- Válassza ki a negyedik példát! Ez az exponenciális függvényt és az inverzét, a logaritmus naturalist, azaz a természetes alapú (e alapú) logaritmus függvényt mutatja.
Az inverz deriváltja (azaz a logaritmus naturalis deriváltja):
.
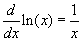Jegyezze meg, hogy mivel az ln(x) csak a pozitív x-eken értelmezett, ezért a deriváltja is csak pozitív x-eken lesz értelmezve!
- Válassza ki az ötödik példát! Ez a 10-es alapú exponenciális függvényt és az inverzét, a 10-es alapú logaritmust mutatja.
Az e-től különböző alapú logaritmus deriválási formulája:
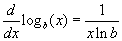, ahol ismét x > 0.
- Válassza ki a hatodik példát, mely a szinuszgörbét és az inverzét, az arcsin(x) függvényt mutatja (amit szoktunk sin-1(x)-nek is írni)!
Itt most az inverz függvény tartományát le kellett szűkítenünk ahhoz, hogy az invertálás egy függvényt eredményezzen, és az x csúszkát is erre a szűkebb tartományra korlátoztuk.
Vizsgálja meg önállóan a többi példát, melyek a tirgonometrikus függvények és inverzeik deriváltjait mutatják (sajnos a grafikai szoftver nem teszi lehetővé az arccot és az arccsc függvények megjelenítését)!
A tirgonometrikus függvények inverzeinek a deriváltjai:
.
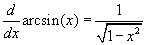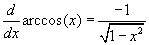
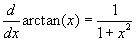
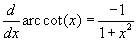
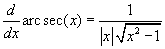
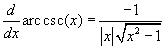
- Ön is megadhat további példákat, de jegyezze meg, hogy mind a függvény, mind az inverzének képletét be kell írnia, mivel
a szoftver nem elég okos ahhoz, hogy az inverz képletét kiszámolja.
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
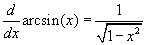