Improprius integrálok
Mi történik akkor, ha az egyik integrációs határ végtelen? Van ilyenkor az integrálnak értke? Vagyis mi lehet az értéke, ha az integrációs határral tartunk a végtelenhez? Ezeket az eseteket a határérték segítségével tudjuk tárgyalni. Például, ha egy olyan határozott integrál értékét szeretnénk megkapni, amelynél az egyik határ végtelen, akkor érdemes azt egy változóval jelölni és venni az integrál határértékét e változó szerint, amint az tart a végtelenhez: 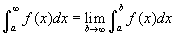 . Ezek után meg kell keresni a primitív függvényt, be kell helyettesíteni a két határt és végül megvizsgálni, hogy létezik-e a határérték. Hasonlóan tegyük fel, hogy egy fügvény az x = b-ben végtelenhez tart (azaz van egy függőleges aszimptotája ebben a pontban). Ebben az esetben is hasonlóan járhatunk el az integrál kiszámításánál:
. Ezek után meg kell keresni a primitív függvényt, be kell helyettesíteni a két határt és végül megvizsgálni, hogy létezik-e a határérték. Hasonlóan tegyük fel, hogy egy fügvény az x = b-ben végtelenhez tart (azaz van egy függőleges aszimptotája ebben a pontban). Ebben az esetben is hasonlóan járhatunk el az integrál kiszámításánál: 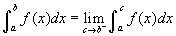 (feltételeztük, hogy a < b, tehát balról tartunk b-hez határértékben). Hasonlóan tudjuk az alsóhatár probémát is kezelni. Ha mindkét határ esetén fennáll a probléma, vagy a két határ közötti részen jelenik meg a problémás rész, akkor két részre tudjuk bontani az integrált, úgy hogy csak az egyik problémás határ legyen az egyik itegrálban.
(feltételeztük, hogy a < b, tehát balról tartunk b-hez határértékben). Hasonlóan tudjuk az alsóhatár probémát is kezelni. Ha mindkét határ esetén fennáll a probléma, vagy a két határ közötti részen jelenik meg a problémás rész, akkor két részre tudjuk bontani az integrált, úgy hogy csak az egyik problémás határ legyen az egyik itegrálban.
Próbálja ki a következőket!
- Az applet bevezetőként egy egyenest mutat. Szeretnénk tudni, hogy
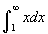 -nek van-e értéke. Szimbolumokkal leírva a következőt tesszük:
-nek van-e értéke. Szimbolumokkal leírva a következőt tesszük: 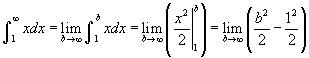 . Az utolsó határérték nem létezik, mivel a függvény nem korlátos. Ez jól látható az appleten is, egy táblázatot is talál a bal felső sarokban, amely b különböző értékeihez megadja az integrál értékét. Amint b egyre nagyobb lesz, egyre nagyobb lesz az integrál értéke is. A grafikonról az is látszik, hogy, amint b nagyobb lesz (mozgassa a b csúszkát), a terület végtelenhez tart.
. Az utolsó határérték nem létezik, mivel a függvény nem korlátos. Ez jól látható az appleten is, egy táblázatot is talál a bal felső sarokban, amely b különböző értékeihez megadja az integrál értékét. Amint b egyre nagyobb lesz, egyre nagyobb lesz az integrál értéke is. A grafikonról az is látszik, hogy, amint b nagyobb lesz (mozgassa a b csúszkát), a terület végtelenhez tart.
- Nézzük a 2. példát, amelyben egy parabola jelenik meg! Hasonlóan az előző példához, ahogy b növekszik, egyre nagyobb lesz a terület:
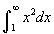 sem korlátos. Belátható, hogy a hatványfüggvények intgrálja 1-től végtelenig, nem korlátos, ha a kitevő nagyobb mint 1. Emlékeztető: az ilyen számok mint például 1.2345E6 tudományos jelölés (normál alak), és 1,2345 x 106-ot jelent.
sem korlátos. Belátható, hogy a hatványfüggvények intgrálja 1-től végtelenig, nem korlátos, ha a kitevő nagyobb mint 1. Emlékeztető: az ilyen számok mint például 1.2345E6 tudományos jelölés (normál alak), és 1,2345 x 106-ot jelent.
- Nézzük a 3. példát! Ebben példában a hatványfügvény reciprokát vizsgáljuk. Vegye észre, hogy amint b egyre nagyobb lesz, a terület 1-hez tart. Valóban, ha vesszük a primitív fügvényt és kiszámoljuk a határértéket, akkor 1 lesz az integrál értéke. Az ilyen integrálra azt mondjuk, hogy konvergens, míg a fenti példában, ahol a határérték nem létezik, azt mondjuk divergens.
- Nézzük a 4. példát, amely egy másik hatványfüggvény reciprokát mutatja! Ennek integrálja konvergens vagy divergens?
Mit gondol, mi törénik, ha nagyobbak a kitevők?
- Nézzük az 5. példát, amelyben a négyzetgyök függvény szerepel (a hatványfüggvényben a kitevő 0,5)! Konvergens lesz vagy divergens?
- Nézzük a 6. példát, amelyben a hiperbola látható, azaz az 1 kitevőjű hatványfüggvény reciproka! Konvergens vagy divergens lesz ez az integrál? Amennyiben növeljük a p kitevő értékét, akkor a következő típusú integrálok
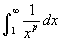 esetén elmondhatjuk, hogy konvergens ha p > 1 és divergens ha p ≤ 1.
esetén elmondhatjuk, hogy konvergens ha p > 1 és divergens ha p ≤ 1.
- Nézzük a 7. példát, amely esetén meg szeretnénk határozni az
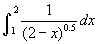 integrál értékét! Ebben az esetben az a probléma, hogy az x = 2-ben az integrandus végtelen lesz. Ezt az esetet is tudjuk kezelni a határérték segítségével "óvatosan megközelítve" 2-t balról. A táblázat mutatja az értékeket, és látható, hogy az értékek 2-höz konvergálnak (amely az integrál értéke).
integrál értékét! Ebben az esetben az a probléma, hogy az x = 2-ben az integrandus végtelen lesz. Ezt az esetet is tudjuk kezelni a határérték segítségével "óvatosan megközelítve" 2-t balról. A táblázat mutatja az értékeket, és látható, hogy az értékek 2-höz konvergálnak (amely az integrál értéke).
- Nézzük a 8. példát, ahol az előző példához képest a kitevő 2! Konvergens vagy divergens lesz az integrál?
- Nézzük a 9. példát! Próbálja ki saját függvényét! Tudja változtatni a-t ahogy szeretné, tud kicsinyíteni, nagyítani és mozgatni a grafikont, valamint b értékét lehet változtatni a táblázatban (kettőt kell klikkelnie a táblázat celláira, így tudja az adatokat változtatni; a változtatás után nyomjon Enter-t). Megjegyezzük, hogy ha túl nagy számot választ b-nek (azaz nagyobbat, mint 1000), akkor az appletnek időre lesz szüksége, hogy az értékeket újra számolja.

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.
![]() . Ezek után meg kell keresni a primitív függvényt, be kell helyettesíteni a két határt és végül megvizsgálni, hogy létezik-e a határérték. Hasonlóan tegyük fel, hogy egy fügvény az x = b-ben végtelenhez tart (azaz van egy függőleges aszimptotája ebben a pontban). Ebben az esetben is hasonlóan járhatunk el az integrál kiszámításánál:
. Ezek után meg kell keresni a primitív függvényt, be kell helyettesíteni a két határt és végül megvizsgálni, hogy létezik-e a határérték. Hasonlóan tegyük fel, hogy egy fügvény az x = b-ben végtelenhez tart (azaz van egy függőleges aszimptotája ebben a pontban). Ebben az esetben is hasonlóan járhatunk el az integrál kiszámításánál: ![]() (feltételeztük, hogy a < b, tehát balról tartunk b-hez határértékben). Hasonlóan tudjuk az alsóhatár probémát is kezelni. Ha mindkét határ esetén fennáll a probléma, vagy a két határ közötti részen jelenik meg a problémás rész, akkor két részre tudjuk bontani az integrált, úgy hogy csak az egyik problémás határ legyen az egyik itegrálban.
(feltételeztük, hogy a < b, tehát balról tartunk b-hez határértékben). Hasonlóan tudjuk az alsóhatár probémát is kezelni. Ha mindkét határ esetén fennáll a probléma, vagy a két határ közötti részen jelenik meg a problémás rész, akkor két részre tudjuk bontani az integrált, úgy hogy csak az egyik problémás határ legyen az egyik itegrálban. 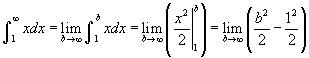 . Az utolsó határérték nem létezik, mivel a függvény nem korlátos. Ez jól látható az appleten is, egy táblázatot is talál a bal felső sarokban, amely b különböző értékeihez megadja az integrál értékét. Amint b egyre nagyobb lesz, egyre nagyobb lesz az integrál értéke is. A grafikonról az is látszik, hogy, amint b nagyobb lesz (mozgassa a b csúszkát), a terület végtelenhez tart.
. Az utolsó határérték nem létezik, mivel a függvény nem korlátos. Ez jól látható az appleten is, egy táblázatot is talál a bal felső sarokban, amely b különböző értékeihez megadja az integrál értékét. Amint b egyre nagyobb lesz, egyre nagyobb lesz az integrál értéke is. A grafikonról az is látszik, hogy, amint b nagyobb lesz (mozgassa a b csúszkát), a terület végtelenhez tart.