A határérték szemléletes fogalma
Egy f függvény valamely bemenő értékre meghatározott értéket vehet fel.
Pédául ha f (x) = 0.5x, akkor f (5) = 2.5. Folytonos függvényeknél, amilyen ez is,
ahogy az x közelít 5-höz, úgy közelít az f (x) függvényérték a 2.5-hez. Ugyanakkor bizonyos egyéb függvényekre is
kiterjeszthetjük ezt a fogalmat, amikor a függvény nem folytonos, vagy nincs értelmezve az adott helyen.
Szemléletesen azt mondjuk, hogy ha f (x) egy L számhoz közelít, amikor x egy c számhoz közelít,
akkor az L értéket határértéknek nevezzük. Matematikailag ezt így írjonuk le: 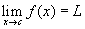 .
.
Próbálja ki a következőket:
- Az első grafikon a fenti példában szereplő egyenest mutatja. A határérték L = 0.5, ha c = 1 ?
Más szóval, ahogy az x közelít az 1-hez, úgy közelít az f (x) a 0.5-hez?
Tolja el az x csúszkát úgy, hogy az x egyre közelebb kerüljön 1-hez! Ebben a példában a határérték 0.5.
Ténylegesen f (1) = 0.5 ebben az esetben, de mint látni fogjuk, ennek nem kell szükségképpen így lennie.
- Válassza ki a második példát! Ez ugyanaz, mint az első, csak épp az egyik pontját áthelyeztük.
Vajon a határérték még mindig L = 0.5, ha c = 1 ? Más szóval, ahogy az x közelít az 1-hez, úgy közelít az f (x) a 0.5-hez?
Mozdítsa el az x csúszkát úgy, hogy az x egyre közelebb kerüljön 1-hez! A határérték ebben a példában is 0.5.
Ahogy x egyre közeledik c = 1-hez, úgy kerül egyre közelebb f (x) az L = 0.5-hez.
A határérték nem 1.5, dacára annak, hogy a függvény az x = 1 helyen ezt az értéket veszi fel.
A határérték nem ez, hanem az a kimenő érték, amelyhez a függvényértékek közelítenek, amikor a bemenő értékek közelítenek 1-hez.
Azon függvények esetében, amelyek a kérdéses pont környezetében folytonosak, mint az első példánál, könnyű megtalálni a határértéket:
csupán ki kell számolnia az illető bemenetre a függvényértéket, hiszen amihez a kimenő értékek közelítenek, az megegyezik a függvénynek
az illető pontban felvett kimenő értékével. A második példához hasonló esetekben a határérték még mindig létezik, csak éppen más szám lesz,
mint a függvényérték.
- Válassza ki a harmadik példát! Ez hasonlít az előző kettőhöz, csak most a függvénynek hiányzik egy pontja (azaz hézagpontja van).
Vajon a határérték még mindig L = 0.5, ha c = 1 ? Más szóval, ahogy az x közelít az 1-hez, úgy közelít az f (x) a 0.5-hez?
Tolja el az x csúszkát úgy, hogy az x egyre közelebb kerüljön 1-hez! A határérték ebben a példában is 0.5.
Ahogy x közeledik c = 1-hez, úgy közeledik f (x) az L = 0.5-hez. Dacára annak, hogy a függvény az x = 1 helyen nem vesz fel semmilyen értékét,
továbbra is létezik itt érvényes határérték, hiszen a függvény egy meghatározott kimenő értékhez közelít.
- Válassza ki a negyedik példát! Ez egy összetettebb függvény, de annyiban hasonlít az előzőhöz, hogy ennek is hézagpontja van.
Mi a határérték, ha c = 0 ? Más szóval, ha az x közelít a 0-hoz, milyen értékhez közelít az f (x)?
Tolja el az x csúszkát úgy, hogy az x egyre közelebb kerüljön 0-hoz! Ebben a példában a határérték 1.
Ahogy x egyre közeledik c = 0-hoz, úgy kerül egyre közelebb f (x) az L = 1-hez.
Dacára annak, hogy a függvény az x = 0 helyen nem vesz fel semmilyen értékét, továbbra is létezik itt érvényes határérték,
hiszen a függvény egy meghatározott kimenő értékhez közelít.
Matematikailag ezt a következőképpen írhatjuk fel:
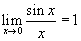 .
.
A határérték része a differenciálszámítás elméleti megalapozásának. A határérték arra is lehetőséget nyújt, hogy
a folytonosság szemléletes meghatározását matematikailag szabatosabb formába öntsük.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
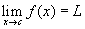 .
.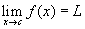 .
.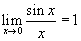 .
.