Egyoldali és kétoldali határérték, és a határérték hiánya
Előfordulhat, hogy egy függvénynek nincs határértéke valamely bemenő értékre. A következő példák néhány ilyen esetet mutatnak be.
Próbálja ki a következőket:
- Az első grafikon egy szakadásos függvényt mutat. Mi a határérték, ha c = 1?
Más szóval, ha x közelít 1-hez, milyen értékhez közelít f (x)?
Tolja el az x csúszkát úgy, hogy az x egyre közelebb kerüljön 1-hez!
Mint látja, f (x) 1-hez közelít, ha x balról közelít az 1-hez,
de f (x) 2-höz közelít, ha x jobbról közelít az 1-hez. Baloldali határértéknek nevezzük, és
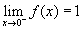 írásmóddal jelöljük azt az esetet, amikor
negatív irányból (balról) közelítünk. Jobboldali határértéknek nevezzük, és
írásmóddal jelöljük azt az esetet, amikor
negatív irányból (balról) közelítünk. Jobboldali határértéknek nevezzük, és 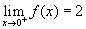 írásmóddal jelöljük azt az esetet, amikor pozitív irányból (jobbról) közelítünk. Ha a baloldali és a jobboldali határértékek
különböznek egymástól (mint jelen esetben), akkor azt mondjuk, hogy f (x)-nek nincs határértéke a c helyen.
Ha a baloldali és a jobboldali határértékek léteznek és azonosak, akkor azt mondjuk, hogy létezik határérték.
írásmóddal jelöljük azt az esetet, amikor pozitív irányból (jobbról) közelítünk. Ha a baloldali és a jobboldali határértékek
különböznek egymástól (mint jelen esetben), akkor azt mondjuk, hogy f (x)-nek nincs határértéke a c helyen.
Ha a baloldali és a jobboldali határértékek léteznek és azonosak, akkor azt mondjuk, hogy létezik határérték.
- Válassza ki a második példát! Ennek a függvénynek van egy függőleges aszimptotája. Mi a határérték, ha c = 1?
Más szóval, milyen értékhez közelít f (x), ha x 1-hez közelít? Tolja el az x csúszkát
úgy, hogy az x egyre közelebb kerüljön 1-hez! Mint látja, f (x) mindkét irányból végtelenhez tart.
Ebben az esetben vagy azt mondjuk, hogy a határérték végtelen, vagy azt, hogy nem létezik, hiszen a végtelen nem szám.
Néha ezt írjuk:
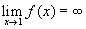 , hogy jelezzük, a határérték azért nem létezik, mert végtelen.
, hogy jelezzük, a határérték azért nem létezik, mert végtelen.
- Válassza ki a harmadik példát! Ez a függvény, a sin(1/x), rendkívüli tekergőzésbe kezd az origó környékén.
Ha a c csúszkát az x = 0 közelébe viszi, láthatja, hogy az y érték össze-vissza ugrál.
Zoomoljon bele és próbálkozzon ismét! Minél jobban belenyagyít a grafikonba, annál tekergőzőbbnek tűnik közelről
(valójában persze nem lesz tekergőzőbb, hanem a grafikai szoftver felbontóképességének vannak korlátai, így a zoomolásnál
csupán többet mutat meg a sűrűn sorjázó hullámokból). Ennek a függvénynek nincsen határértéke a c = 0 helyen, mivel semmilyen konkrét értékhez nem közelít.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
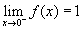 írásmóddal jelöljük azt az esetet, amikor
negatív irányból (balról) közelítünk. Jobboldali határértéknek nevezzük, és
írásmóddal jelöljük azt az esetet, amikor
negatív irányból (balról) közelítünk. Jobboldali határértéknek nevezzük, és 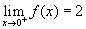 írásmóddal jelöljük azt az esetet, amikor pozitív irányból (jobbról) közelítünk. Ha a baloldali és a jobboldali határértékek
különböznek egymástól (mint jelen esetben), akkor azt mondjuk, hogy f (x)-nek nincs határértéke a c helyen.
Ha a baloldali és a jobboldali határértékek léteznek és azonosak, akkor azt mondjuk, hogy létezik határérték.
írásmóddal jelöljük azt az esetet, amikor pozitív irányból (jobbról) közelítünk. Ha a baloldali és a jobboldali határértékek
különböznek egymástól (mint jelen esetben), akkor azt mondjuk, hogy f (x)-nek nincs határértéke a c helyen.
Ha a baloldali és a jobboldali határértékek léteznek és azonosak, akkor azt mondjuk, hogy létezik határérték.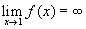 , hogy jelezzük, a határérték azért nem létezik, mert végtelen.
, hogy jelezzük, a határérték azért nem létezik, mert végtelen.