Kalkulus Appletek

Sorok

A számsor egy számsorozat tagjainak az összegét jelenti. Például a 2, 4, 6, 8, ... sorozat részösszegei 2, 6, 12, 20, ...lesznek. Ezek a részösszegek véges sorok. Az n-edik részösszeget általában S_n-el jelöljük. Ha az s_n-eket adjuk össze, akkor a részösszeg jelölése: 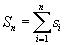, amely azt jelenti, hogy az s sorozat első n elemét adjuk össze. Amennyiben a sorozat végtelen sok tagját adjuk össze, akkor végtelen számsort kapunk.

Próbálja ki a következőket!

1. Az applet azt a számtani sorozatot ábrázolja, ahol s_n = s₁ + d(n - 1), az s₁-et és a d-t úgy választjuk, hogy a páratlan egész számokat adja a sorozat. A grafikonon a sorozatot téglalalpok ábrázolják, melyeknek a szélessége 1, ez a Riemann összegre emlékeztet. Az első tagja a sorozatnak 1, így az első téglalap 1 magasságú és 1 szélességű. A második tag a példában 3, így a következő téglalap 3 magasságú és 1 szélességű, a harmadik tag 5 magasságú és 1 szélességű, és így tovább. A pontok reprezentálják a grafikonon a részösszegeket, ezek értékét a sorozat tagjainak összege adja, ahol a tagok számát a pont helye adja meg. Vizuálisan azt jelenti, hogy a pontok magassága egyenlő azon téglalalpok területének összegével, amelyek a ponttól balra helyezkednek el. Így az első pont koordinátája (1,1), a másodiké (2,3), a harmadiké (3,5), stb. A csúszkával, vagy beírással változtathatja az s₁ és d értékét. A bal felső sarokban a táblázat néhány nagy értéket mutat a sorozatból és a véges sor értékeiből, világosan látszik, hogy a végtelen sor divergál.
   
   
2. Nézzük a 2. példát a legördülő listáról, amely egy mértani sorozatot ábrázol s_n = s₁r^{n - 1} ahol s₁ = 1 és r = 2! Látható, hogy a végtelen sor itt is divergens. Változtassa r értékét a csúszka segítségével, úgy hogy az |r| < 1 feltétel teljesüljön. Ekkor úgy tűnik, hogy a sor konvergens lesz. Mi töténik, ha r < -1? Azt láttuk, hogy a mértani sorozat konvergens lesz, ha |r| < 1 és hasonló igaz a mértani sorra is. A képlete egy véges mértani számsornak 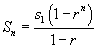, míg egy konvergens végtelen mértani sornak 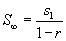. Néhány tankönyv n=0 értékkel kezd 1 helyett, így a részösszegek formulája kicsit másképp néz ki. Ha ezt látja a táblázatban "undefined" (meghatározhatatlan) azt jelenti, hogy túl nagy a kiválasztott szám abszolútértéke.
   
   
3. Nézzük a 3. példát, amely s_n = (n + 1)/n! Itt a sorozat 1-hez konvergál, de a végtelen sor divergens, mert amint n egyre nagyobb lesz egy 1-hez közeli értékű számot kell az összeghez hozzáadni, tehát határ nélkül növekszik. Az általános tag divergencia-teszt azt állítja, ha egy sorozat egy zérustól különböző értékhez konvergál, akkor a számsor divergens. Matematikailag, ha 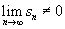, akkor a számsor divergens.
   
   
4. Nézzük a 4. példát, amelyben a harmonikus sor látható! Ennek definíciója: 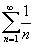. A sorozat zérushoz konvergál, de figyelve a táblázatot, nem világos, hogy a sor konvergens vagy nem. Hasonlóan a pontokat figyelve a grafikonon az y = ln(x) függvényhez hasonlít, amelyről tudjuk, hogy nem konvergens. Tény, hogy a harmonikus sor divergens; határok nélkül lassan növekszik. Vegye észre, hogy az átalános tag divergencia-teszt csak azt mondja, ha a sorozat egy nem-zérus értékhez konvergál, akkor a sor divergens. Azt nem állítja, hogy mi történik, ha a sorozat zérushoz konvergál. Ebben az esetben a sor vagy konvergál vagy nem, attól függ, hogy milyen gyorsan tart a sorozat nullához. A harmonikus sorozat konvergál zérushoz, de nem elég gyorsan ahhoz, hogy a sor is konvergens legyen.
   
   
5. Nézzük a 5. példát, amely a p-sort mutatja, ami 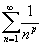! Ha p = 1, akkor a harmonikus sort, az előző példát kapjuk, amelyről tudjuk, hogy nem konvergens. Mozgassa p csúszkáját, és figyelje mi történik ha p > 1, 0 < p < 1, és p < 0! Ezek közül melyik esetben következik be, hogy a p-sor konverges? Vegye észre, hogy a p-sor konvergens, ha p > 1 és divergens a többi esetben!

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.