A kalkulus második alaptétele
Előzőekben már láttuk a kalkulus alatételét, amely ezt állítja: ha f folytonos függvény az [a,b] intervallumon, akkor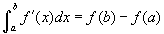 
. Más szavakkal, egy függvény deriváltjának a határozott integrálja visszaadja az eredeti függvényt. Mi történik akkor, ha megcseréljük a sorrendet és a határozott integrál deriváltját vesszük? Ha az integrációs határok konstansok, ez az eset nem túl érdekes, mivel az integrál értéke konstans, így a deriváltja zérus lesz. Amennyiben a határotott integrál egy integrálfüggvényt reprezentál (az integál, mint felsőhatár függvény), akkor azt kapjuk, amit a kalkulus második alaptételének szoktunk nevezni: 
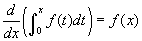. Szavakkal megfogalmazva, egy egyszerű integrálfüggvény deriváltja visszaadja az integrandust, csak a változó jele cserélődik ki (t szerepelt az integrandusban az integrál jel mögött, megkülönböztetve a felső határon szereplő x-től).
Próbálja ki a következőket!
- Az applet 3 grafikont mutat: f (t) grafikonját a bal oldalon,
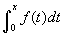grafikonját középen, 
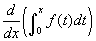grafikonját a jobb oldalon. Az a(x) reprezentálja az alsó határt (ebben a példában 0), míg b(x) reprezentálja a felső határt (ennél a példánál x). Mozgassa az x csúszkát és figyelje mi történk a bal oldali grafikonon. Amint megváltoztatja x-et, b is megváltozik (mivel x-től függ). A terüet színezve látható (a pozitív terület zöld, a negatív terület piros). A középső grafikon az integrálfüggvényt mutatja, amely a területet ábrázolja az x függvényében (vagyis y a terület a bal oldalon). A középső grafikonon ugyancsak látható az érntő egyenes egy adott x értékhez, és a bal felső sarokban jelzi a meredekségét az egyenesnek. A jobb oldali grafikon kirajzolja ezt a meredekséget az x függvényében, azaz ez a deriváltja az integrálfüggvénynek. Vegyük észre, hogy ez a függvény éppen úgy néz ki, mint a bal oldali grafikon kivéve azt, hogy itt x a változó t helyett. Így megtalálhatjuk könnyen az integrálfüggvény deriváltját, csak ki kell cserélni a változót az integrandusban, ahogy ezt a kalkulus második alaptételében már megfogalmaztuk. Egy másik úton is megközelíthetjük a problémát, mégpetdig a kalkulus alaptétele alapján, ahogy ezt korábban már láttuk. Ha az f (x) primitív függvénye F (x), akkor 
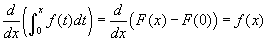. Az F (0) deriváltja eltűnik, mivel konstans, és konstans deriváltja zérus.
- Nézzük a 2. példát a legördülő listáról, amely a sin(t) függvényt mutatja, mint integrandust! Mozgassa az x csúszkát és figyelje a területet, amit a középső grafikonon x függvényében ábrázolunk, és a jobb oldali grafikon kirajzolja a középső függvény meredekségét! Ebben az esetben is egyezik a bal és a jobb oldali grafikon.
- Nézzük a 3. példát! Ebben a példában újra egyenes van, de a felső határ most 2x. Világosan látszik, hogy a jobb oldali grafikon ebben az esetben már nem teljesen egyezik meg a bal oldali grafikonnal. Mi történik? Mozgassa az x csúszkát és figyelje mi történik b-vel. Mivel a felső határ nem x, hanem 2x, b kétszer olyan gyorsan változik, mint x, és így nagyobb terület lesz színezve. Azaz a középső parabola meredekebb, és így a derváltja egy meredekebb egyenes lesz. Mennyivel meredekebb? Használjuk a deriválási módszert az első példa alapján:
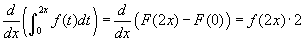. Itt a t, az integrandus változóját 2x-re kell kicserélni, de van még egy szorzó a 2, amelyet a láncszabály alapján kapunk, amikor F (2x) deriváltját számoljuk. Amikor kiszámoljuk az integrálfüggvény deriváltját, ahol a felső határ nem csupán egy egyszerű változó, egy kicsit több munkára van szükségünk.
- Nézzük a 4. példát! Ebben a példában egy egyenest látunk integrandusként és a felső határ x². Mozgassa az x csúszkáját és figyelje b-t, amely mindig pozitív, amint ezt elvátjuk az x² következményeként! Számoljunk a következoképpen:
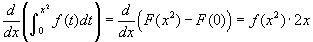! Behelyettsítettük a felső határt x²-et a t helyére az inegrandusban, és megszoroztuk (a láncszabály következményeként) 2x-el (amely az x² deriváltja).
- Nézzük az 5. példát! Ebben a példában az alsó határ is változik. Mozgassa az x csúszkát és figyelje mindkettőt, a-t és b-t hogyan változnak, ha x változik. Az előzőekhez hasonlóan számolhatunk:
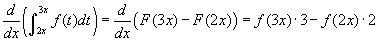. Ebben a példában az alsó korlát sem konstans, így két részből áll elő az eredmény, amelyeket ki kell vonni egymásból. Az első részt úgy kapjuk, hogy az integrandusba a felső határt helyettesítettük be t helyére és megszoroztuk a felső határ deriváltjával (a láncszabály miatt), a második részt úgy, hogy az integrandusba az alsó határt helyettesítjük be a t helyére és ezt ugyancsak megszorozzuk az alsó határ derivátjával.
This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.