Kalkulus Appletek

Az utazás során megtett távolság becslése a sebesség ismeretében, táblázat használatával

Tegyük fel, hogy egy autó halad az úton különböző időpontokban adott sebességgel. Hogyan tudná közelítőleg meghatározni az autó által megtett távolságot a kezdeti helytől a végpontig?

Próbálja ki a következőket!

1. Az applet egy táblázatot mutat, adott sebességekkel, melyeket feet/s-ban (láb/s) mérünk. A első példa t = 0 és t = 8 (1. sor) között mutatja a v(t) sebességeket (2.sor). Az autó köztes sebességeiről nem tudunk semmit. Amint az látható az autó 20 láb/s sebességgel halad végig. Csak feltételezni tudjuk, hogy az autó sebessége az első 8 másodpercben végig ugyanakkora (a feltételezett sebességet a 3. sor mutatja), így a távolság amit az autó megtesz 8 s szorozva 20 láb/s azaz 160 láb (1 láb kb 30,48 cm), ezt a táblázat utolsó sorai mutatják .
   
   
2. Változtassa meg az intevallumok számát 2-re (azaz cserélje ki az 1-et 2-re az Intervals ablakban és nyomja le az Enter-t)! Ekkor megjelenik néhány többlet adat a t = 4s-ban, ez azonban nem hoz változást a távolság tekintetében az előző esethez képest. Tegyük fel, hogy az első 4 s -ban az autó 20 láb/s -mal halad és hasonlóan a 2. intervallumban (4 és 8 s között) is 20 láb/s-mal; a feltételezett sebességet a 3. sor mutatja a táblázatban, "velocity" megjelöléssel. Így a teljes távolság éppen 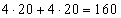láb. Az intervallumok számát lehet növelni, de ezekben az esetekben az autó valójában végig konstans sebességgel halad, így tudjuk, hogy a megtett távolság mindig 160 láb lesz.
   
   
3. Nézzük a 2. példát a legördülő listáról! Ebben az esetben az autó 20 láb/s sebességgel rendelkezik a t = 0-ban, de 76 láb/s sebessége lesz a t = 8 s-ban. Mit kellene használni feltételezett sebességnek az intervallumban? Az egyik lehetőség, hogy a kezdeti sebesség legyen végig (azaz a felsorolt sebességből a bal oldalit "left"-et választjuk), így feltesszük, hogy az autó sebessége az egész intervallumban konstans és egy pillanat alatt gyorsul fel a végső sebességre. Ez azt jelenti, hogy a becsült távolság 160 láb. Feltehetjük azt is, hogy a jobb oldali sebességgel, a nagyobb sebességgel halad végig az intevallumban, vagyis az elején egy pillanat alatt felgyorsul 76 láb/s-ra. Ekkor a "right" -ot kell válsztni az ablakban a "left" helyett, így a távolság 608 láb lesz. Micsoda különbség!
   
   
4. Hogyan kaphatnánk egy jobb közelítést a megtett útra? Különböző megközelítések lehetnek a 8 s alatt, egy újabb meközelítés lehet, ha több sebességmintát választunk. Írjuk be a 2-t az Intervals ablakba és nyomjunk Enter-t. Azt látjuk, hogy a sebesség a t = 4 s-ban 64 láb/s. Két intervallum van, 4 s hosszúságú mindkettő, az első intervallumban a kezdő ("left") sebességet vagy a végsebességet ("right") sebességet választjuk, mint feltételezett sebességet az egész intervallumra. Használjuk a választási ablakban a bal vagy a jobb oldali sebességet (ne válasszunk kisebb és nagyobb esetet most) és figyeljük mi történik a táblázatban! Változtatva a bal vagy a jobb oldali sebességet mindkét intervallumban, változtatva a feltételezett sebességet, a 4. sor (amely az egyes intervallumokhoz tartozó távolságokat mutatja, ez egyszerűen a sebesség szorozva az idő intervallum hossza), és az 5. sor (amely a teljes távolságot mutatja). Vegyük észre, hogy a "left" teljes és a "right" teljes út közötti különbség kisebb, mint az egy intervallumos esetben. Több adat segít csökkenteni a különbséget a ténylegesen megtett út és a becsült út között.
   
   
5. Állítsa be az intervallumok számát 4-re, és üssön Enter-t! Vizsgáljuk meg a left (bal) és a right (jobb) eseteket! Mit veszünk észre? Probáljuk ki 8, 16, és nagyobb intervallumszámra is! Egy bizonyos értéknél a táblázat már nem mutatja az adatokat, mert túl sok oszlop lenne, de a teljes utat kiírja. Mi történik azzal a különbséggel, amelyet a left és a right választás estén adódó távolságokból számolunk? Bizonyosodjon meg 4 intervallumos esetben, hogy érti-e hogyan kell kiszámolni a 2. sor adataiból a 3. és a 4. sor adatait!
   
   
6. Nézzük a 3. példát a legördülő listáról! Itt a 2 intervallumos esettel kezdjük és vegyük észre, hogy az autó 10 láb/s sebességgl indul, majd lelassít 2 láb/s-ra, és utána újra felgyorsít 90 láb/s-ra. Ki lehet választani a left vagy a right esetet, hogy megnézze a távolság közelítését. Most azonban két stratgiánk is van kiválasztani a sebességet egy-egy intervallumhoz. Ki lehet válaszatni a kisebb sebességet a kezdő és a végpontbeli sebességek közül, vagy a nagyobbat. Az előző példában ez a left és a right válaztásoknak felelt meg, mivel az autó végig gyorsított a 8s alatt. De ez az autó először lassít, majd gyorsít, így a kisebb és a nagyob sebesség nem esik egybe a bal és a jobb esetekkel. Válasszuk ki a lesser (kisebb) vagy a greater (nagyobb) sebességet és figyeljük, hogy mi lesz a sebesség a 3. sorban! Hasonlítsuk össze a left és lesser, majd a right és greater eseteket!
   
   
7. Változtassa meg az intervallumok számát 4-re majd nyomjunk Enter-t! Amint az előzőekben a left és right esetekben a különbség a teljes távolságok között kisebb lett, itt is a lesser és a greater esetek között a teljes távolságok különbsége kisebb lesz. Próbálja ki nagyobb intervallumszámmal és nézze meg mi történik! Próbálja ki 1000 intervallumra! Közeledik a teljes megtett út az eljárás során egy bionyos számhoz?
   
   
8. Nézzük a 4. példát a legördülő listáról! Ebben az esetben az autó álló helyzetből indul (a sebesége zérus). A t = 4s-ban az autó elindul visszafelé, ezt jelenti a negatív sebesség. A t = 8s-ban az autó újra előre halad 90 láb/s-os sebességgel. Ha mindkét intervallumban a left, azaz a bal oldali sebességeket választjuk, akkor úgy becsüljük, hogy az autó az első intervallumban nem mozog, mivel azt tettük fel, hogy a sebesség 0 láb/s az első 4s-ban. A második 4s-ban a -8 láb/s-os sebességet választjuk, így az autó visszafelé halad -32 lábnak megfelelő távolságot. A teljes távolság tehát a kezdeti helytől -32 láb, ez azt jelenti, hogy az autó hátrébb lesz 32 lábbal ahhoz képest ahonnan indult. Megjegyezzük, hogy ez a távolság nem az, amit a távolságmérő óra mutatna, ami minden megtett utat pozitívnak mutat. Ahhoz, hogy megkapjuk ezt a mért értéket, minden intervallumnak az abszolút értékét vesszük.
   
   
9. Próbálja ki 4, 8 és több intervallumra ezt a példát, és left, right, lesser és greater választási lehetőségeket az egyes intervallumok sebességeinek megválasztásakor!
   
   
10. Nézzük az 5. példát a legördülő listáról! Ez a lehetőség megengedi, hogy a sebsség függvényt definiáljuk, így saját példáit is kipróbálhatja. Szerkeszteni tuja a sebességfüggvény definícióját (amelyben a t-t tekintjük változónak), az indulás pillanatát, a megállás pillanatát, és az intervallumok számát.

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.