Mozgás síkon
A kalkulust felhasználhatjuk annak megértéséhez is, hogy hogyan mozog egy tárgy egy kétdimenziós sík felületen.
Ekkor egy paraméteres egyenletpárral, azaz x(t) és y(t) egyenletekkel írjonuk le
a tárgy helyzetét a síkban t időpontban.
E két függvény t szerinti deriváltjai fogják megadni a tárgy sebességének x és y
irányú összetevőit, azaz vx(t) = x'(t) és vy(t) = y'(t).
A gyorsaságot, vagyis a sebesség nagyságát a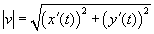 
képlet adja meg.
Ne felejtse el, hogy a sebesség egy vektor, azaz nagysága és iránya is van.
Hasonlóan, a gyorsulásnak is két összetevője lesz, ax(t) = x''(t) és ay(t) = y''(t),
a nagyságát pedig a 
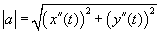képlettel számoljuk ki.
Próbálja ki a következőket:
- Az applet először egy körmozgást mutat a síkon (ha a kör képe elnyúlt, kattintson az Equalize Axes gombra).
A fekete pötty a mozgó tárgyat jelöli, a lila görbe pedig a pályáját, amit paraméteresen adunk meg.
Kattintson a Start gombra az animáció elindításához! A grafikon kijelzi a |v| és |a| értékeket,
melyek jelen esetben konstansak és mindegyik 1-gyel egyenlő. A sebességvektort kék nyillal jelöltük
(a nyil a fekete pöttyből indul ki), a gyorsulásvektort pedig piros nyillal.
Mikor mozog a tárgy az x-tengellyel párhuzamosan? Akkor, amikor a sebességvektor is párhuzamos az x-tengellyel.
Tolja el a csúszkát és keresse meg ezt a pontot! A választ úgy is megadhatja, ha meghatározza azt az értéket, ahol vy(t) = y'(t) = 0
(azaz ahol a sebesség y irányú összetevője 0). Az applet azt mutatja, hogy y'(t) = cos t.
Ezt egyenlővé téve nullával és megoldva t értékeire azt kapjuk, hogy π/2 páratlan számú többszörösei a megoldások.
- Válassza ki a második példát, mely egy jóval bonyolultabb mozgást mutat a síkon! Kattintson a Start gombra az animáció elindításához!
Melyik időpontban áll meg a tárgy? A csúszka elhúzásával megbecsülheti ezt az időpontot.
Egzaktabban úgy határozhatjuk meg ezt, hogy kiszámoljuk, mely időpontban lesz x'(t) is és y'(t) is nulla.
Más szóval meghatározzuk ezt a két deriváltat, egyenlővé tesszük őket nullával, majd megoldjuk az egyenleteket.
A tárgy minden alkalommal áll ezen egyenletek t megoldásaira. Jelen esetben a t = 1 időpontot kapjuk.
Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.