Forgástestek térfogata
Megnéztük hogyan határozzuk meg két görbe által közrefogott terület, úgy hogy téglalap szeleteket adunk össze, majd integrálunk az integrációs határokkal. Hasonló elgondolást alkalmazhatunk, ha egy olyan térfogatot akarunk meghatározni, amelyet úgy kapunk, hogy két görbe közötti területet megforgatunk egy tengely körül.
Próbálja ki a következőket!
- Az applet elsőként egy olyan területet ábrázol, amelyet két egyenes az f (x) = 2 és a g(x) = 0 határol, ahol az intervallum x = 0-tól x = 2-ig tart. Ha a sárga téglalapot megforgatjuk az x tengely körül, akkor egy hengert kapunk. A sárga területen sötét szürke színben látható a kicsi téglalap szelet. Ha ezt megforgatjuk az x tengely körül, akkor egy korongot kapunk, amely világos szürke színben látható. Jól ismerjük a korong térfogatát, amit V = π r² h összefüggés ad meg. Ahol h a vékony henger magassága, ez a mi esetünkben most dx. A sugara a sárga téglalap magassága, amely jelen esetben 2. Így a szürke korong térfogatata π 2²dx = 4πdx. A teljes térfogata a hengernek
 , amely ismereteinkkel megegyező eredmény.
, amely ismereteinkkel megegyező eredmény.
- Nézzük a 2. példát a legördülő listáról! Ebben a példában az egyetlen változás az, hogy f (x) = x. Mozgassa az x csúszkát és figyelje hogyan változik a korong sugara! A sugár az f aktuális x-hez tartozó értéke, speciálisan most x. Így az integrál
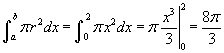 , amely ugyancsak megerősíti az ismert geometriai össefüggést a kúpra.
, amely ugyancsak megerősíti az ismert geometriai össefüggést a kúpra.
- Nézzük a 3. példát a legördülő listáról, amely az f (x) =x² függvényt mutatja. Mozgassa x csúszkáját, hogy megnézze hogyan változik a sugár x változásának következményeként! Ebben a példában a korong sugara x², tehát az integrál
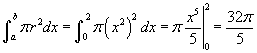 . Összefoglalásul, amikor a forgástengely és az alsó függvény megegyezik és éppen az x tengely, akkor az inegrál
. Összefoglalásul, amikor a forgástengely és az alsó függvény megegyezik és éppen az x tengely, akkor az inegrál 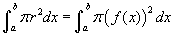 .
.
- Nézzük a 4. példát, ahol egy hengert látunk egy lyukkal (hétköznapi szóhasználattal: cső)! Ez az első példa ahol g(x) = 1. A sárga télalap nem a forgástengelytől indul, ezért lesz egy lyuk a henger közepén. A szürke korong pedig egy alátétgyűrű lesz. A legegyszerűbb módja, hogy a gyűrű területét megadjuk, ha a korong területéből kivonjuk a lyuk területét. Már ismerjük a külső henger térfogatát (lásd az 1. példát). A lyuk integrálja is hasonló, csak kisebb a sugár. Tehát:
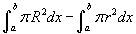 , ahol R ("nagy R") a külső sugár és r ("kis r") a lyuk sgara. Ebben a példában kapjuk:
, ahol R ("nagy R") a külső sugár és r ("kis r") a lyuk sgara. Ebben a példában kapjuk: 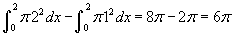 .
.
- Nézzük az 5. példát, amely egy hengert ábrázol egy kúp alakú lyukkal! Húzza az x csúszkát és figyelje a gyűrűt x változása függvényében! A külső R sugár 2, mint az előbb, de most a belső r (a lyuk sugara) változik g(x) = x alapján. Így az integrál:
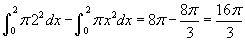 .
.
- Nézzük a 6. példát, amely egy egyedi alakot mutat, amit az x tengely körül forgattunk meg! Mozgassa az x csúszkát, hogy benyomása legyen arról a testről, amit a sárga terület forgatásával kapunk! A két integrál kükönbségeként kapjuk:
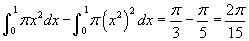 .
.
- Nézzük a 7. példát! Itt is egy egyedi alakzatot látunk. Ebben a példában a függvények és a tengely ugyanazok, mint az előző példában, csak az integrációs határok lettek eltolva. Vegye észre, hogy ami változott az a külső R sugár és a belső r sugár! Ha ugyanazt a számolást használnánk, mint az előbb, akkor negatív térfogatot kapnánk. Ahhoz, hogy pozitív térfogatot kapjunk ki kell cserélnünk R-et, hogy ez a tengelytől távolabbi sugarat jelentse. Így az integrál:
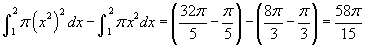 .
.
- Nézzük a 8. példát, az előző függvényekkel, de másik forgástengellyel, mely y = 1! Mozgassa az x csúszkát, hogy a forgatással kapott test alakját el tudja képzelni! Az R ebben az esetben a tengelytől a g(x)-ig tartó távolság, így R = 1 -x². Hasonlóan r (a lyuk sugara) a tengely távolsága f (x)-től, azaz r = 1 - x. Így az inetegrál:
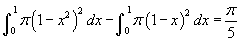 . Vegye észre, hogy a zárójel használata biztosítja az R és r helyes négyzetre emelését!
. Vegye észre, hogy a zárójel használata biztosítja az R és r helyes négyzetre emelését!
- Nézzük a 9. példát! Az előző területet látjuk, amit most a függőleges tengely körül forgatunk meg. A függvények most y függvényei x helyett. Mozgassa y csúszkáját, hogy megnézze a gyűrű változását! A test alakja egy tálra hasonlít. Az integrál:
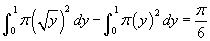 . A területet hasonlóan kell megforgatni a függőleges tengely körül, mint ahogy a vízszintes tengely körül. Vegye észre, hogy a térfogatra más eredményt kapunk, mint a 6. példában (ahol ugyanezt az alakot forgattuk meg az x tengely körül)!
. A területet hasonlóan kell megforgatni a függőleges tengely körül, mint ahogy a vízszintes tengely körül. Vegye észre, hogy a térfogatra más eredményt kapunk, mint a 6. példában (ahol ugyanezt az alakot forgattuk meg az x tengely körül)!
- Nézzük a 10. példát! Itt kipróbálhatja saját függvényét, válsszon tengelyt, és változtassa a határokat! Tudja használni az "inverse" ablakot, ahol függőleges tengelyt választhat, de ekkor újra kell írnia a függvényt y-t használva x helyett.

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.
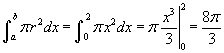 , amely ugyancsak megerősíti az ismert geometriai össefüggést a kúpra.
, amely ugyancsak megerősíti az ismert geometriai össefüggést a kúpra. 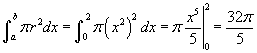 . Összefoglalásul, amikor a forgástengely és az alsó függvény megegyezik és éppen az x tengely, akkor az inegrál
. Összefoglalásul, amikor a forgástengely és az alsó függvény megegyezik és éppen az x tengely, akkor az inegrál 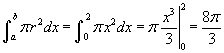 , amely ugyancsak megerősíti az ismert geometriai össefüggést a kúpra.
, amely ugyancsak megerősíti az ismert geometriai össefüggést a kúpra. 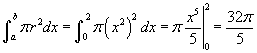 . Összefoglalásul, amikor a forgástengely és az alsó függvény megegyezik és éppen az x tengely, akkor az inegrál
. Összefoglalásul, amikor a forgástengely és az alsó függvény megegyezik és éppen az x tengely, akkor az inegrál 