L'Hopital szabály
Tegyük fel, hogy meg szeretnénk határozni 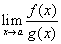 értékét az f (a) = g (a) = 0 feltétel mellett.
Ennek egyik módszerét a L'Hopital szabály adja meg, mely a következőt állítja: ha f (x) és g (x) differenciálható függvények és f (a) = g (a) = 0, akkor
értékét az f (a) = g (a) = 0 feltétel mellett.
Ennek egyik módszerét a L'Hopital szabály adja meg, mely a következőt állítja: ha f (x) és g (x) differenciálható függvények és f (a) = g (a) = 0, akkor 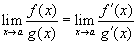 , feltéve hogy a jobboldali határérték létezik.
Más szóval az eredeti határértéket úgy kapjuk meg, hogy meghatározzuk a számlálóban és nevezőben álló függvények deriváltjai hámnyadosának a határértékét.
A következő appletben azt próbáljuk megértetni, hogy miért működik ez a szabály.
, feltéve hogy a jobboldali határérték létezik.
Más szóval az eredeti határértéket úgy kapjuk meg, hogy meghatározzuk a számlálóban és nevezőben álló függvények deriváltjai hámnyadosának a határértékét.
A következő appletben azt próbáljuk megértetni, hogy miért működik ez a szabály.
Próbálja ki a következőket:
- Az applet baloldalán a
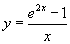 grafikonját látja.
Ez a függvény nincs értelmezve az x = 0 pontban, de eléggé nyilvánvalónak tűnik, hogy van határértéke e pontban.
Ha bevezetjük az f (x) = e2x - 1 és g (x) = x jelöléseket,
alkalmazhatjuk a L'Hopital szabályt, vagyis a határértéket meghatározhatjuk a számláló és nevező deriváltjai hányadosának határértékéből.
Íme:
grafikonját látja.
Ez a függvény nincs értelmezve az x = 0 pontban, de eléggé nyilvánvalónak tűnik, hogy van határértéke e pontban.
Ha bevezetjük az f (x) = e2x - 1 és g (x) = x jelöléseket,
alkalmazhatjuk a L'Hopital szabályt, vagyis a határértéket meghatározhatjuk a számláló és nevező deriváltjai hányadosának határértékéből.
Íme: 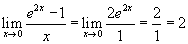 .
Jegyezze meg, hogy nem a hányados deriváltját vesszük a hányadosra vonatkozó deriválási szabály szerint, hanem
külön-külön deriváljuk a számlálóban és a nevezőben álló függvényeket, majd meghatározzuk a hányadosuk határértékét.
Figyelje meg, hogy míg az eredeti hányados nem értelmezhető az x = 0 helyen, a deriváltak hányadosa már igen,
így a határértéket kiszámolhatjuk pusztán úgy, hogy helyettesítjük az x = 0 értéket!
.
Jegyezze meg, hogy nem a hányados deriváltját vesszük a hányadosra vonatkozó deriválási szabály szerint, hanem
külön-külön deriváljuk a számlálóban és a nevezőben álló függvényeket, majd meghatározzuk a hányadosuk határértékét.
Figyelje meg, hogy míg az eredeti hányados nem értelmezhető az x = 0 helyen, a deriváltak hányadosa már igen,
így a határértéket kiszámolhatjuk pusztán úgy, hogy helyettesítjük az x = 0 értéket!
Miért működik ez a módszer? A jobboldali grafikon f (x)-et és g (x)-et mutatja.
Ha rákattint néhányszor a Zoom In gombra, a lokális linearitás miatt a görbe egyre hasonlóbbá válik egy egyeneshez.
Ezért a függvényeket közelíteni tudjuk az x = 0 pontbeli érintőjükkel (vagyis f (x) ≈ 2x és g(x) ≈ x),
a hányadosukat pedig közelíteni tudjuk ezen érintők hányadosával. Végső soron ez az érintők meredekségének az arányával, azaz pontosan a számláló és nevező deriváltjainak a hányadosával lesz egyenlő.
- Válassza ki a második példát a legördülő menüből! Ez egy másik példa:
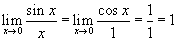 .
Ha most megint rákattint néhányszor a Zoom In gombra a grafikonok ismét kiegyenesednek és a hányadost ki tudjuk számolni a deriváltértékek hányadosának segítségével.
.
Ha most megint rákattint néhányszor a Zoom In gombra a grafikonok ismét kiegyenesednek és a hányadost ki tudjuk számolni a deriváltértékek hányadosának segítségével.
- Válassza ki a harmadik példát, mely ezt mutatja:
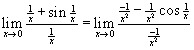 .
Ebben az esetben a jobboldali határérték nem létezik, így a L'Hopital szabályt nem tudjuk alkalmazni.
.
Ebben az esetben a jobboldali határérték nem létezik, így a L'Hopital szabályt nem tudjuk alkalmazni.
- A L'Hopital szabály abban az esetben is működik, ha f (a) = g (a) = ∞, illetve ha
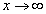 .
.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
![]() értékét az f (a) = g (a) = 0 feltétel mellett.
Ennek egyik módszerét a L'Hopital szabály adja meg, mely a következőt állítja: ha f (x) és g (x) differenciálható függvények és f (a) = g (a) = 0, akkor
értékét az f (a) = g (a) = 0 feltétel mellett.
Ennek egyik módszerét a L'Hopital szabály adja meg, mely a következőt állítja: ha f (x) és g (x) differenciálható függvények és f (a) = g (a) = 0, akkor ![]() , feltéve hogy a jobboldali határérték létezik.
Más szóval az eredeti határértéket úgy kapjuk meg, hogy meghatározzuk a számlálóban és nevezőben álló függvények deriváltjai hámnyadosának a határértékét.
A következő appletben azt próbáljuk megértetni, hogy miért működik ez a szabály.
, feltéve hogy a jobboldali határérték létezik.
Más szóval az eredeti határértéket úgy kapjuk meg, hogy meghatározzuk a számlálóban és nevezőben álló függvények deriváltjai hámnyadosának a határértékét.
A következő appletben azt próbáljuk megértetni, hogy miért működik ez a szabály.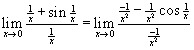 .
Ebben az esetben a jobboldali határérték nem létezik, így a L'Hopital szabályt nem tudjuk alkalmazni.
.
Ebben az esetben a jobboldali határérték nem létezik, így a L'Hopital szabályt nem tudjuk alkalmazni.