Paraméteres deriváltak
Korábban találkoztunk már olyan görbékkel, melyeket az y = f (x) függvénydefinícióval adtunk meg.
Meg tudunk azonban adni összetettebb görbéket is, melyek az x és y között olyan összefüggést fejeznek ki, amelyek nem definiálhatók paraméteres egyenleteket tartalmazó függvényképletekkel.
A paraméteres görbéket két külön függvény, x(t) és y(t) segítségével adjuk meg, ahol az egyes
függvények a megfelelő x és y koordinátákat jelölik, és egy bevezetett t paramétertől függnek.
Ahogyan t változik, úgy változnak a görbe pontjainak x és y koordinátái.
Így például az y = x² görbét paraméteres alakban így írhatjuk fel: x(t) = t és y(t) = t².
A bonyolultabb görbék képletében bonyolultabb x(t) függvények fognak szerepelni.
Egy paraméteres görbe esetében, ha meg szeretnénk határozni az y változásának mértékét x-hez képest
(más szóval a görbe x szerint első deriváltját), továbbá ha meg szeretnénk határozni ennek deriváltját
(azaz a második deriváltat), a következő képleteket alkalmazhatjuk:
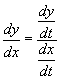 és
és 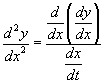 .
.
Figyelje meg, hogy mind a két deriváltat a t paraméter szerinti deriválálásból nyerjük!
Próbálja ki a következőket:
- Az applet első példája egy paraméteres alakban megadott kör grafikonját mutatja
(ha a kör elnyúltnak tűnik, kattintson az Equalize Axes gombra). Jelen esetben x(t) = cos(t) és y(t) = sin(t).
Mozgassa a t csúszkát, mellyel megváltoztathatja a t paraméter értékét!
A t változásával az x(t) és y(t) értékek, azaz a görbe pontjainak a koordinátái
is megváltoznak (amit a lila pötty mozgásán követhet). A t változtatásával a pötty végigjára a görbét.
A határpont-szerkesztő panel most kiegészült néhány további mezővel, melyeken nyomon követhetjük a görbe felírásában szereplő t parméter minimum- és maximumértékeit (tmin és tmax),
továbbá azt, hogy hány részintervallumra osztottuk fel a t intervallumot
(tintervals: ha ezt a számot kisebbre állítjuk, a görbe grafikonja szögletesebbé válik).
A grafikonról leolvasható a dy/dx érték is, mely az aktuális t értéknek megfelelő pontban meghúzott érintőnek a meredeksége.
Ezt a fenti képlettel számoljuk ki, így:
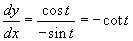 .
A grafikon kijelzi a második derivált értékét is,
melyet a fenti képlettel így számolunk ki:
.
A grafikon kijelzi a második derivált értékét is,
melyet a fenti képlettel így számolunk ki: 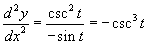 .
.
- Válassza ki a második példát a legördülő menüből! Ez is egy kör, amit most az x(t) = cos(2t) és y(t) = sin(2t) képlet ad meg.
Mozgassa a t csúszkát és nézze meg, mi történik!
Milyen változással jár a szinusz és koszinusz függvényekbe beleírt 2-es szorzó? Hogyan változik a grafikon?
Hogyan változik a pont helyzete, ha t-t változtatja? Hogyan változik a derivált?
A paraméteres görbék többször végigfuthatnak önmagukon, szemben az y = f (x) képlettel megadott görbékkel.
- Válassza ki a harmadik példát a legördülő menüből! Ez egy egyenes.
A tmin = 0 and tmax = 1 beállítás miatt az egyenesnek csak egy részét mutatjuk. Mint már bizonyára kitalálta, dy/dx konstans,
hiszen a fenti képletek alapján
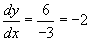 .
.
- Válassza ki a negyedik példát a legördülő menüből! Ez egy ellipszis, melynek egyenletei csak egy apró eltérést mutatnak a köréhez képest.
Ki tudja számolni a deriváltakat?
- Válassza ki az ötödik példát, mely egy Lissajous alakzatot mutat!
Most a t szorzója más a szinusz függvény argumentumában és más a koszinuszéban. Mozgassa a t csúszkát és
Próbálja meg megérteni, hogy a görbe miért azt az utat járja be, amit bejár!
- Ön is kipróbálhat saját példákat, ha t más függvényeit írja be x(t) és y(t) helyére, és a tmin, tmax értékeket megfelelően beállítja.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
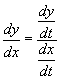 és
és 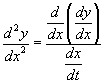 .
.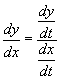 és
és 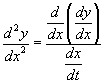 .
.