Egymással összefüggő mértékek: az olvadó hógolyó
A differenciálszámítás egy másik alkalmazása a változások gyorsaságának a követése.
Tegyük fel például, hogy van egy 70 cm sugarú hógolyónk, melynek olvadásakor a sugara konstans módon, percenként 2 centiméterrel csökken.
Milyen gyorsan csökken a hógolyó térfogata?
Próbálja ki a következőket:
- Az applet a hógolyót ábrázolja a kiinduló 70 cm-es sugárral. A térfogatváltozás mértékét meghatározhatjuk úgy, hogy
felállítunk egy egyenletet a térfogatra, ebbe beleírjonuk a sugár változását az idő függvényében kifejező formulát,
és így megkapjuk azt a formulát, amely a térfogat változását az idő függvényében fejezi ki.
Mint tudjuk, a gömb térfogatát a
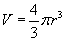 képlet adja meg.
Mivel a hógolyó 70 cm-es sugárról indul és 2 cm per perccel zsugorodik, ezért
képlet adja meg.
Mivel a hógolyó 70 cm-es sugárról indul és 2 cm per perccel zsugorodik, ezért 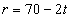 ,
ahol t azt a percekben számolt időt jelöli, ami az olvadás kezdete óta eltelt. Ha r-t behelyettesítjük a
a V képletébe, azt kapjuk, hogy
,
ahol t azt a percekben számolt időt jelöli, ami az olvadás kezdete óta eltelt. Ha r-t behelyettesítjük a
a V képletébe, azt kapjuk, hogy 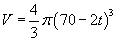 .
Ez a kifejezés fel van tüntetve az appleten. Ha ezt t szerint deriváljuk, azt kapjuk, hogy
.
Ez a kifejezés fel van tüntetve az appleten. Ha ezt t szerint deriváljuk, azt kapjuk, hogy 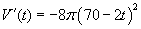 ,
ami szintén látható az appleten (az egyszerűsítést megelőző formában).
Most tetszőleges t értéket beírhatunk ebbe a képletbe, hogy kitaláljuk, milyen mértékben csökken a térfogat.
Kattintson rá a Start gombra az appleten! Elindul az animáció a t idő 0 pillanatától a 35. percig haladva
(amikor a hógolyó eltűnik). A grafikon tetején V(t), az alján V ' (t) látható.
A grafikon mutatja a V(t), r(t), V ' (t) és r' (t) értékeket is.
Figyelje meg, hogy ebben a példában r' (t) konstans!
Ha azt szeretnénk megtudni, hogy mekkora a térfogatváltozás mértéke, amikor a hógolyó sugara 20 cm,
csupán be kellene írnunk 20-at az r helyére az r képletében, és meg kellene oldalunk az egyenletet t-re
(azt kapnánk, hogy t = 25, ha r = 20), majd ezután be kellene írnunk ezt a t-t a V ' képletébe.
Az appleten akár le is futtathatja az animációt (a lejátszás sebességét Moderate-ről Slow-ra csökkentve),
figyelve az r értékét, és a Pause gombra kattintva, amikor r = 20, vagy közel annyi.
Ekkor beírhat más t értékeket, egészen addig, amíg azt nem találja, hogy r = 20,
amikor már csak a kijelzőn látható V ' értéket kell leolvasnia.
,
ami szintén látható az appleten (az egyszerűsítést megelőző formában).
Most tetszőleges t értéket beírhatunk ebbe a képletbe, hogy kitaláljuk, milyen mértékben csökken a térfogat.
Kattintson rá a Start gombra az appleten! Elindul az animáció a t idő 0 pillanatától a 35. percig haladva
(amikor a hógolyó eltűnik). A grafikon tetején V(t), az alján V ' (t) látható.
A grafikon mutatja a V(t), r(t), V ' (t) és r' (t) értékeket is.
Figyelje meg, hogy ebben a példában r' (t) konstans!
Ha azt szeretnénk megtudni, hogy mekkora a térfogatváltozás mértéke, amikor a hógolyó sugara 20 cm,
csupán be kellene írnunk 20-at az r helyére az r képletében, és meg kellene oldalunk az egyenletet t-re
(azt kapnánk, hogy t = 25, ha r = 20), majd ezután be kellene írnunk ezt a t-t a V ' képletébe.
Az appleten akár le is futtathatja az animációt (a lejátszás sebességét Moderate-ről Slow-ra csökkentve),
figyelve az r értékét, és a Pause gombra kattintva, amikor r = 20, vagy közel annyi.
Ekkor beírhat más t értékeket, egészen addig, amíg azt nem találja, hogy r = 20,
amikor már csak a kijelzőn látható V ' értéket kell leolvasnia.
- A térfogatváltozás mértékét másféleképpen úgy határozhatjuk meg, hogy a térfogatképletet még azelőtt deriváljuk, hogy behelyettesítenénk a képletbe
az r egyenletét.
Válassza ki a második példát az applet tetején lévő legördülő menüből! Most V-t is és r-t is t függvényében tekintjük,
így a térfogatképlet ilyen alakú lesz:
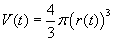 .
Ha ezt t szerint deriváljuk a láncszabály alkalmazásával, ezt kapjuk:
.
Ha ezt t szerint deriváljuk a láncszabály alkalmazásával, ezt kapjuk: 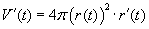 .
Mindkét képlet látható az appleten (a derivált most sincs egyszerűbb alakra hozva).
Tegyük fel, hogy V '-t nem egy adott időpontban szeretnénk meghatározni, hanem akkor, amikor r = 20.
Ehhez ez a formulánk a használhatóbb, hiszen beírhatunk 20-at r(t) helyére és -2-t r'(t) helyére,
anélkül hogy bármit is tudnunk kéne t-ről.
.
Mindkét képlet látható az appleten (a derivált most sincs egyszerűbb alakra hozva).
Tegyük fel, hogy V '-t nem egy adott időpontban szeretnénk meghatározni, hanem akkor, amikor r = 20.
Ehhez ez a formulánk a használhatóbb, hiszen beírhatunk 20-at r(t) helyére és -2-t r'(t) helyére,
anélkül hogy bármit is tudnunk kéne t-ről.
- Válassza ki a harmadik példát! Mi van akkor, ha továbbra is V ' értékét szeretnénk meghatározni az r = 20 érték mellett,
de most csak annyit tudunk r '-ről, hogy -3-mal egyenlő r = 20 esetén? Más szóval
nem ismerjük az r (t) formulát. Tudunk-e még válaszolni a kérdésre? Igen, ha felhasználjuk az előzőekben felírt
V ' (t) formulát, mely független az r formulájára vonatkozó ismeretünktől.
Nem kell mást tennünk, mint beleírni az r értékét és az ehhez tartozó r ' értéket.
A grafikus megoldás megkereséséhez állítsa az animáció sebességét Slow-ra, majd a Start gombbal indítsa el!
Figyelje a kijelzőn az r értékét, és kattintsonon rá a Pause gombra, amikor r 20 körül jár!
Ekkor kezdjen el t értékeket beírni, amíg azt nem kapja, hogy r = 20 (ötlet: próbálja ki a t = 8.35175311 értéket).
Immár csak le kell olvasni V ' értékét a kijelzőn.
Az ilyen típusú problémákat hívjuk related rates problémáknak, azaz összefüggő mértékekkel kapcsolatos problémáknak, mivel
ismerünk egy változási mértéket és meg akarunk találni egy vele összefüggő másik változási mértéket.

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
