Kalkulus Appletek

Hányadoskritérium

A hányadoskritérium nagyon hasznos a konvergencia meghatározásra, mert nagyon egyszerű. Tegyük fel, hogy van egy sor ahol a_n pozitív. Ha , akkor ha N < 1 a sor konvergens, ha N > 1 a sor divergens, és ha N = 1 nem tudjuk eldönteni , hogy divergens vagy konvergens.

Próbálja ki a következőket:

1. Az applet a következő sort mutatja: . A grafikonról és a táblázatból is egyértelműn úgy tűnik, hogy konvergens, mégpedig egészen gyorsan konvergál (az "undefined" megjelenése a táblázatban az n! következménye, túl naggyá válik az értéke, amely már meghaladja a változó számértékbeli tárolási kapacitását). A hánydoskritérium szerint meg kell néznünk az egymást követő tagok hányadosát, hogyan viselkedik amint n egyre nagyobb lesz: . 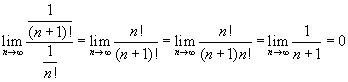Mivel a határérték < 1, a sor konvergens.

This work by Thomas S. Downey is licensed under a Creative Commons Attribution 3.0 License.