Szakaszonként definiált függvény folytonossá és differenciálhatóvá tétele
Azok a szakaszonként definiált függvények, melyek megadásában paraméter szerepel, csak a paraméter biznyos értékeire lesznek folytonosak és differenciálhatóak.
Ez az applet azt mutatja be, hogy mit jelent ez a grafikon szempontjából.
Próbálja ki a következőket:
- Az első példa a következő szakaszonként definiált függvényt mutatja:
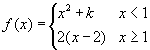 .
A k = 0 kezdőértéknél a függvény nem folytonos az x = 1 pontban, amint az kitűnik a grafikonról.
Van olyan k érték, melyre a függvény folytonossá válik az x = 1 pontban? Próbálja mozgatni a k csúszkát,
vagy írjon be egy választott értéket a k mezőbe.
Hogyan alkalmazná algebrai ismereteit, hogy kiszámolja k-t a függvény képletéből?
Gondolja át, mit csinált a grafikon szempontjából (megpróbálta a függvény két részét az x = 1 pontban összekapcsolni).
Hogyan tudná ezt egyenletben kifejezni, melyet aztán megoldhatna k-ra?
Az ábrára kattintva bele is nagyíthat azon pont környezetébe, ahol a két darabnak kapcsolódnia kellene egymáshoz.
.
A k = 0 kezdőértéknél a függvény nem folytonos az x = 1 pontban, amint az kitűnik a grafikonról.
Van olyan k érték, melyre a függvény folytonossá válik az x = 1 pontban? Próbálja mozgatni a k csúszkát,
vagy írjon be egy választott értéket a k mezőbe.
Hogyan alkalmazná algebrai ismereteit, hogy kiszámolja k-t a függvény képletéből?
Gondolja át, mit csinált a grafikon szempontjából (megpróbálta a függvény két részét az x = 1 pontban összekapcsolni).
Hogyan tudná ezt egyenletben kifejezni, melyet aztán megoldhatna k-ra?
Az ábrára kattintva bele is nagyíthat azon pont környezetébe, ahol a két darabnak kapcsolódnia kellene egymáshoz.
- Válassza ki a második példát, mely egy másik szakaszonként definiált függvényt mutat:
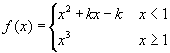 .
Ez a függvény folytonos az x = 1 pontban, de nem differenciálható itt a k = 0 érték mellett,
amint azt leolvashatja az első derivált grafikonjáról.
Van olyan k érték, melyre a függvény differenciálhatóvá válik az x = 1 pontban?
Tologassa a k csúszkát, hogy megpróbáljon ilyet találni!
Ki tudja-e számolni valahogyan a függvényanalízis és az algebra alkalmazásával ezt a k értéket a függvény képletéből?
Gondolja át, mit csinált a grafikon szempontjából (megpróbálta a függvény két részének meredekségét egyformává tenni az x = 1 pontban)!
Hogyan tudná ezt egyenletben kifejezni, melyet aztán megoldhatna k-ra?
.
Ez a függvény folytonos az x = 1 pontban, de nem differenciálható itt a k = 0 érték mellett,
amint azt leolvashatja az első derivált grafikonjáról.
Van olyan k érték, melyre a függvény differenciálhatóvá válik az x = 1 pontban?
Tologassa a k csúszkát, hogy megpróbáljon ilyet találni!
Ki tudja-e számolni valahogyan a függvényanalízis és az algebra alkalmazásával ezt a k értéket a függvény képletéből?
Gondolja át, mit csinált a grafikon szempontjából (megpróbálta a függvény két részének meredekségét egyformává tenni az x = 1 pontban)!
Hogyan tudná ezt egyenletben kifejezni, melyet aztán megoldhatna k-ra?

Szerző: Thomas S. Downey. Szerzői jog: Creative Commons Attribution 3.0 License.
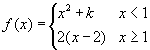 .
A k = 0 kezdőértéknél a függvény nem folytonos az x = 1 pontban, amint az kitűnik a grafikonról.
Van olyan k érték, melyre a függvény folytonossá válik az x = 1 pontban? Próbálja mozgatni a k csúszkát,
vagy írjon be egy választott értéket a k mezőbe.
Hogyan alkalmazná algebrai ismereteit, hogy kiszámolja k-t a függvény képletéből?
Gondolja át, mit csinált a grafikon szempontjából (megpróbálta a függvény két részét az x = 1 pontban összekapcsolni).
Hogyan tudná ezt egyenletben kifejezni, melyet aztán megoldhatna k-ra?
Az ábrára kattintva bele is nagyíthat azon pont környezetébe, ahol a két darabnak kapcsolódnia kellene egymáshoz.
.
A k = 0 kezdőértéknél a függvény nem folytonos az x = 1 pontban, amint az kitűnik a grafikonról.
Van olyan k érték, melyre a függvény folytonossá válik az x = 1 pontban? Próbálja mozgatni a k csúszkát,
vagy írjon be egy választott értéket a k mezőbe.
Hogyan alkalmazná algebrai ismereteit, hogy kiszámolja k-t a függvény képletéből?
Gondolja át, mit csinált a grafikon szempontjából (megpróbálta a függvény két részét az x = 1 pontban összekapcsolni).
Hogyan tudná ezt egyenletben kifejezni, melyet aztán megoldhatna k-ra?
Az ábrára kattintva bele is nagyíthat azon pont környezetébe, ahol a két darabnak kapcsolódnia kellene egymáshoz. 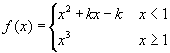 .
Ez a függvény folytonos az x = 1 pontban, de nem differenciálható itt a k = 0 érték mellett,
amint azt leolvashatja az első derivált grafikonjáról.
Van olyan k érték, melyre a függvény differenciálhatóvá válik az x = 1 pontban?
Tologassa a k csúszkát, hogy megpróbáljon ilyet találni!
Ki tudja-e számolni valahogyan a függvényanalízis és az algebra alkalmazásával ezt a k értéket a függvény képletéből?
Gondolja át, mit csinált a grafikon szempontjából (megpróbálta a függvény két részének meredekségét egyformává tenni az x = 1 pontban)!
Hogyan tudná ezt egyenletben kifejezni, melyet aztán megoldhatna k-ra?
.
Ez a függvény folytonos az x = 1 pontban, de nem differenciálható itt a k = 0 érték mellett,
amint azt leolvashatja az első derivált grafikonjáról.
Van olyan k érték, melyre a függvény differenciálhatóvá válik az x = 1 pontban?
Tologassa a k csúszkát, hogy megpróbáljon ilyet találni!
Ki tudja-e számolni valahogyan a függvényanalízis és az algebra alkalmazásával ezt a k értéket a függvény képletéből?
Gondolja át, mit csinált a grafikon szempontjából (megpróbálta a függvény két részének meredekségét egyformává tenni az x = 1 pontban)!
Hogyan tudná ezt egyenletben kifejezni, melyet aztán megoldhatna k-ra?